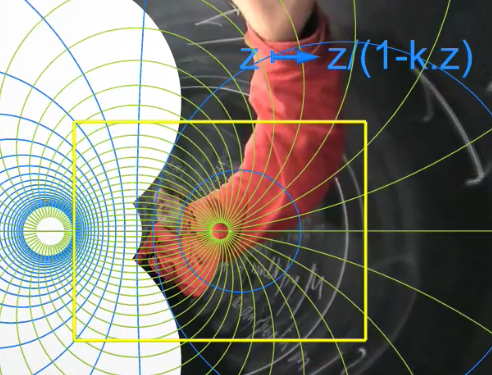
维度数学漫步第6集讲了一种很有意思的图片变换：把一张照片放在复平面上，然后对所有的复数都做一个变换$z\to f(z)$并把这个复数对应的点移动到变换后的位置上，得到一张新的图片。新图看起来就像是原图经过一些扭曲后得到的，虽然它整体上看是“跑形”了但我们仍然可以辨认出图上的内容，比如原图是两个人的合影，变换后你也看得出是两个人的合影，只不过两人都被夸张地扭曲了。这样的变换称为共形变换，或全纯变换。

为什么这种变换会有这样的性质呢？这是因为它是保角的，即一个角在变换前后的大小不变（也许变换后角的边变成了曲线，这时它的大小就该是这两条曲线在顶点处的切线的夹角）。所以，共形变换也叫保角变换。

我在这里写了一个共形变换的程序，大家可以用图片去试着变换一下。

我们下面来看一些简单的变换例子，看一下图片在各种基本函数变换下的形态。

$z\to -{1\over z}$

这个变换叫做复反演变换，影片里面也介绍过了。我们知道，复数的除法就是它的模长相除，幅角相减，所以对于靠近原点的复数变换后模就会变得很大，原点本身被映射到了复无穷上，远离原点的点被压缩到了原点附近。我们看到最终原点以外的点都被图片充满了，只有原点附近的点是空的，这就是那些远离原点的点的像。

$z\to z^2$

这也是影片里面出现过的变换，正是因为它是平方映射，所以直线会被变换成抛物线：

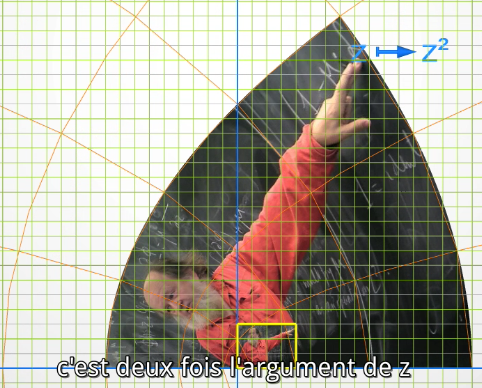
不过，注意照片的左下角，它和原点是重合的，与它相邻的两条边是相互垂直的，而在变换之后这个直角却成了平角！这似乎违背了共形变换的保角性。但看其他地方又是正常的，比如那些变换前后的坐标网格，似乎例外只发生在原点处。其实，我们知道复数的乘法就是模长相乘，幅角相加，那么顶点位于原点处的角在变换后就会变为以前的两倍；而除了原点以外的其他点仍然有保角性。像平方变换这样的保角性不是在全平面成立的变换称为亚纯变换。 其实，数学上保角性只是共形变换的一个必要条件，共形变换的

$z\to e^z$

这是一个很有意思的变换，称为指数映射。影片中数学家的照片在变换后成了一个圆，而且被压得很小，还说“用显微镜就能看到我的头”。

为什么这个变换会有这种性质呢？我们设平面上的一点z为$z=a+bi$，代入变换公式，我们得到像点

也就是说，像的模长为$e^a$，幅角为b。由于照片是矩形的，边界上a或b为常数，所以变换后它就会变成同心扇形，如果照片的左右边界的实部（横坐标）分别为$a_1$和$a_2$，上下边界的虚部（纵坐标）分别为$b_1$和$b_2$，那么大半径和小半径就分别为$e^{a_1}$和$e^{a_2}$，扇形的角度范围是$b_1$到$b_2$。如果照片的宽度超过了$2\pi$那么它变换之后就会是一个同心圆，这就是影片里面的情形。仔细看它的变换动画我们发现照片的右边界是固定的，左边界迅速被压小成一个“点”，也就是说，变换前右边界和y轴是重合的，左边界的横坐标是负的，这样变换后得到的小半径就会被指数映射压得很小。

在图片的右边有一条从原点出发的不连续线，这条线叫做分支割线，这是因为对于实部相同而虚部相差$2\pi$的整数倍的两个点它们的像是相同的，于是我们就人为地规定这个像点的原像是一个虚部在0和$2\pi$内的点，所以就出现了这条不连续的线。

$z\to\ln(z)$

这个变换是指数映射的逆变换，也就是说它会把一个同心扇形变换成一个矩形。

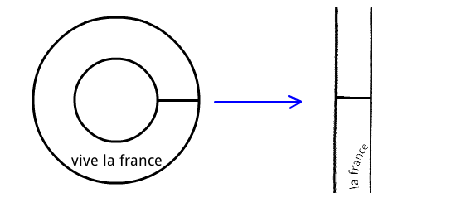
对于一个模长为r，幅角为$\theta$的复数，即$z=re^{i\theta}$，它的对数就是$\ln z=\ln r+i\theta$，角度重新变成了纵坐标。看起来这没什么问题，但是，在变换前给$\theta$加上$2\pi$的整数倍是不影响z的值的，也就是说一个z有多个相应的$\theta$；但在变换后每个$\theta$都会有一个不同的z，所以说对数函数在复数域上是一个多值函数，每个值的虚部都相差$2\pi$的整数倍。这样得到的图就会在纵坐标方向成周期排布。

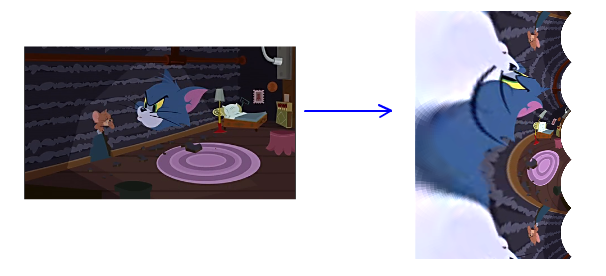
我们看到，对数映射会使图片发生很怪异的扭曲，这也是我经常用它来变换我同学照片的原因（其中有一张我和wxy的合影的对数变换我现在看到都想笑。。。）。

对于一个离原点很近的点，它的模长r就很小，所以变换之后的横坐标$\ln r$就会负得很厉害，所以原点附近的点在变换后就会充满整个图片的左半部分。这就是为什么猫的嘴巴会变得那么扭曲。

$z\to\sqrt{z}$

复数中平方根也是多值函数，因为如果$a$是$\sqrt{z}$的值，那么$-a$也一定是$\sqrt{z}$的值。因此这个变换的结果一定是中心对称的。如果坐标原点在图上面那么变换后的图片就会是像这样的：

如果原点没有落在图上那么变换后的图片就是相互中心对称的两部分：

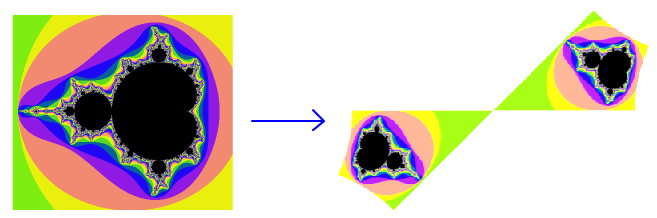
记得上一篇文章里面讲的分形的逆推法吗？当时我们就说过了如果图形移动到了原点以外就会被分成两部分。

$z\to\sin z$

这是一个比较神奇的变换，我们先来看一个例子：

他好像把一个正方形变成了一个椭圆！真是这样吗？我们不妨考虑原图上的一个点$z=t+ia$，它的像点就应该是$z^\prime=\sin(t+ia)=\sin t\cosh a+i\cos t\sin a$。如果我们固定a改变t，就得到一个椭圆，它的半长轴和半短轴分别为$\cosh a$和$\sin a$。有趣的是，当a趋于0，即实轴时，椭圆的半短轴消失了！也就是说实轴这条直线的像是一条长度为2的线段。在这条线段以外就是两条不连续的分支割线，这就是因为两条纵坐标互为相反数的水平直线的像是一样的，我们于是人为地定义纵坐标为正的直线的像为上半椭圆，为负的是下半椭圆，这就造成了这条不连续线。

对于整个变换而言，$\sin z={1\over 2i}(e^{iz}-e^{-iz})$，于是我们就可以把它看成是两个指数变换的叠加。在虚轴的正半轴$e^{-iz}$很快就变得很小，像点主要由$e^{iz}$决定；同样在负半轴$e^{-iz}$就占主导地位。于是整个图片看起来就像是两个指数变换圆滑地拼接成的。

视频里面演示的所有变换都是用一个动画渐变过去的，这是怎么做到的呢？这就需要找到一个新的带一个参数的变换，并且满足当参数从0变化到1时这个变换能平滑地从单位变换变化到原变换。当我们连续地将参数从0变化到1时我们就可以得到一个变换的过渡动画。对于变换$z\to f(z)$而言，我们需要找到一个变换$z\to f(z,a)$，使得$f(z,0)=z$且$f(z,1)=f(z)$。这只是一个必要不充分条件，要找到一个过渡变换我们还需要具体问题具体分析。

我们先从简单的开始。视频的前几个变换都是形如$z\to bz$的变换，图片是一边匀速地缩放一边匀速地变换出来的，为了在渐变变换中体现出这一点，我们需要把b写成指数形式：$b=re^{i\theta}$，这样，过渡变换就是$f(z,a)=(1-a+ar)e^{ia\theta}z$。 那么$z\to z^2$呢？只需注意到那个不保角的点，即原点处的角度变化，我们立即得到$f(z,a)=z^{a+1}$。更一般地，对于变换$z\to z^b$，我们有$f(z,a)=z^{ab+1-a}$。

有意思的是$z\to{-1\over z}$。我们发现两个点$\pm i$在整个过渡过程中都是不动点。另外，我们发现原点的像点在过渡时从原点沿实轴正方向移动到了无穷远处，如果参数是a，那么我们可以写出原点像点为$z={a\over(1-a)}$。那么接下来就是很关键的一步，通过观察坐标网格的变化我们可以确定这个变换是一个分式线性变换，即形如$z\to{az+b\over cz+d}$的变换，这多少靠了一点直觉，因为分式线性变换会把一个圆域变换成圆域或半平面。

这下就简单了，我们只需代入上面的三个点就可以得到过渡变换为$f(z,a)={(1-a)z+a\over -az+1-a}$。

其实我们还可以把那两个不动点改为$\pm 1$，或者改成任意的两个关于原点对称且距离原点为1的两个点，从而得到向任何方向翻转的过渡动画。

大家也许会问，这些共形变换的图片是怎么画出来的呢？如果我们把原图的每一个像素直接搬到一个空白图片相应的像点上就会出现像素在图片上分布不均匀的问题。所以，我们是采用逆变换的方式，即遍历空白图片上的每个像素，找到它的原像并读取原图上相应点的颜色值，然后绘制到空白图片上。这样就可以保证像素是均匀的。另外，为了让图片的效果更好，一般还会加入抗锯齿。