数学中的分形可以说是一种艺术，我们可以通过分形来构造出各种优美的图片，它具有无限精细的结构，可以被无限放大，并且在这些精细结构中还存在缩小了的整个分形！这就是分形的自相似性。当我在维度数学漫步第5集看到Julia集合和Mandelbrot集合时就被它的神奇震撼了，一个简单的变换居然可以创造出如此复杂的分形！下面我们就来讨论一下这个数学上的艺术品吧。

• Julia和Mandelbrot集合的定义
• 颜色方案
• 自相似结构
• 四维Mandelbrot集合
• 在线计算Julia和Mandelbrot集合（点这里）

这两种分形都是定义在复平面上的二维图形，我们知道，复数可以做加减乘除运算，那么就可以对复平面上的点做变换，从而得到一些新的点。现在我们对这些点不断的做这个变换：$z\to z^2+c$，其中c也是一个复数，这样有些点就会离原点越来越远甚至趋于无穷远处，而有些则会一直呆在原点附近。我们把这些在不断的变换中一直在原点附近，即没有跑到无穷远处的点构成的集合就称为Julia集合，简称J集合。比如，c=0时的J集合就是一个单位圆区域，因为模长大于1的复数平方后会变大，小于1的会变小。真正有意思的是c取非零值时候的形状，不过这时只能借助计算机来画julia集合了。不过这也很简单，由于我们不能做到迭代无限次，所以只能用一个有限值来代替，在迭代过程中当复数的模大于某个值（一般取2）的时候就说明这个点没在julia集合里面，我们把顺利完成所有迭代的点在复平面上画出来就得到了J集合的图形。下面我们来看一些例子。

图中的黑色部分就是J集合。为了好看我们给集合之外的点上了色，后面我们会讲具体的上色方式。

我写了一个画J集合和mandelbrot集合的网页程序，更多的例子大家可以去那里看一下，这篇文章中所有的分形图都是这个程序的截图。你可以随意改变c的值，观察J集合的变化，并可以放大它，观察它的精细结构，你就会发现它的自相似性。

那么Mandelbrot集合又是怎么定义的呢？这和julia集合中的c有关。也许你已经发现了，当c取某些值时Julia集合看起来似乎消失了，比如当c=0.26时：

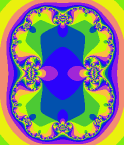
实际上，就像维度中讲的一样，Julia集合分散成了无数个零散的点以至于我们看不见。那么这些使julia集合没有分散的c值构成的集合就称为Mandelbrot集合，简称M集，文章开头的那个图片就是它。我们看到它的最前面有一个向里面的凹槽，其实那个凹槽是无限趋近于c=0.25这个点的。

那么该怎么计算M集合呢？换句话说，给一个任意的c值我们怎么知道它对应的J集合不是一堆零散的点呢？其实只要原点没有发散，J集合就不是零散的。为什么呢？Matrix67的博客上讨论了一种倒推法：既然在画J集合时当模长大于2时就被判定为发散的，那么J集合中的点最终一定会落在了以原点为圆心半径为2的圆中。这样我们就可以对这个圆盘不断的做逆变换——不断的减c再开方——来得到J集合。如果原点不属于J集合，那么在某一次逆变换中原点就会落在图形的外面，这样在开方后图形就会被分成两部分，继续逆变换就会变成4部分、8部分……并且每个部分的面积越来越小，最终这些被分散的部分就成了无数个零散的点。所以，原点不发散就是J集合是连续图形的充要条件，对于每个c，我们只需要取$z_0=0$为检验点就可以判断出c是否属于M集。

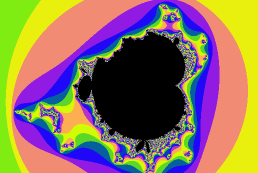
不过，如果我们的检验点选择的是其他的点会怎么样呢？这时我们得到的M集就像是被“咬了一口”一样，比如选择检验点$z_0=0.2+0.5i$：

如果我们放大M集合我们会发现在它的周围有很多看起来和整体很像的“小M集合”：

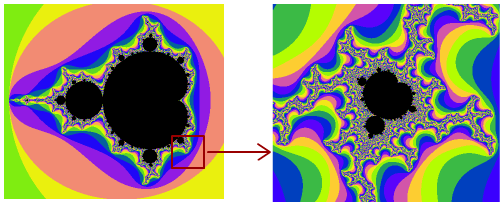
不过仔细看我们发现这个“小M集合”的一半边头比另一半要大一些，这说明M集合不是严格自相似的。

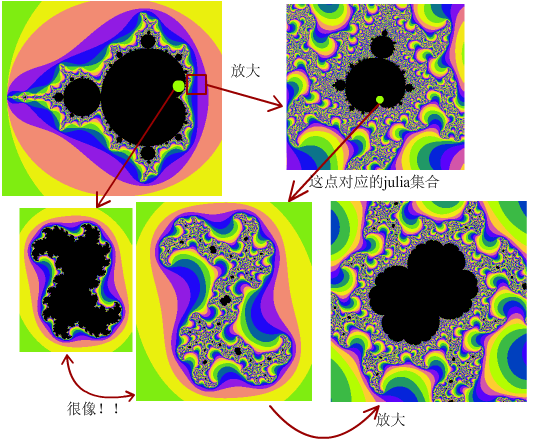
当c的值落在这些小M集合中时它对应的J集合会很有意思：这个J集合也是由很多个小J集合组成的，它们的形状和在大M集合中相应的点对应的J集合一样，比如这里我们在小M集合里面选的点是“凹槽”点，对应大M集合中c=0.25的点。而这些小J集合组成的图形和大M集合中在小M集合附近的点对应的J集很像！这算是它们自相似性的另一种体现。

如果我们把M集合中的那个映射改成$z\to z^n+c$，就得到一种更一般的集合，称为Multibrot集合。我们可以连续的改变n，看Multibrot集合的变化。比如，从0到5：

在前面的图中大家也看到了我们给J集和M集上了色，具体是怎么做的呢？有两类方法：三角函数法和三角不等式法。

三角函数法

上面那些图用的就是这个比较简单的方法：对于复平面上的所有点，如果它属于J集（或M集），那么它的颜色就是黑色，否则它的颜色（RGB值或者HSV）就是一个关于这个点已经迭代了的次数的三角函数。比如我是这样做的：

其中k是迭代次数。这样得到的颜色就具有周期性，我们可以看到分形周围有一圈一圈的颜色层，从外面到里面颜色是周期性变化的。 不过我们这样画出来的颜色变化就比较明显，维基百科上讲了一种使颜色的变化更平滑的方法，就是在计算颜色之前先把迭代次数k处理一下：设此时复数的模为r，那么计算$\phi=\log_2r^2,\nu=\log_2\phi$，那么新的k就是$k\to k+1-\nu$，这时再计算颜色就可以得到平滑变化的颜色了。

三角不等式

我一直想知道维度上的那种M集是怎么画出来的，它的官网上是这样说的：设$z_{n}$是迭代n次得到的复数，那么计算$A=|z_n-z_{n-2}|$，$B=|z_n-z_{n-1}|$以及$C=|z_{n-1}-z_{n-2}|$，那么根据三角不等式，$A/(B+C)$一定是介于0和1之间的，然后再根据这个值在色相环上找颜色。但是它也没说具体怎么找，而且网上也几乎没有介绍这种方法的，无奈去找了一个分形软件的源码来慢慢分析……等我搞懂之后再来更新。

其实M集和J集不仅可以用颜色来表示，还可以表示成三维的！维度作者之一的josleys画出了这样的M集合：

更多的图片可以去这里看。不过josleys也没有讲具体方法，只是简单的说把平面上的距离转化成深度。

既然M集合中的任何一点都有一个J集与它对应，那么有没有办法把它们统一到一起呢？答案是肯定的，不过由于这两个集合都是二维的，把它们“杂交”之后得到的就是一个四维分形了。那么该怎么定义呢？我们希望这个四维分形在一个方向上的截面是J集，在另一个方向上的是M集，所以我们这样定义四维M集：对于空间中的点$(x,y,z,t)$，当点$(x,y)$属于$c=z+it$的J集合时它就属于四维M集。这样它在平行于$Oxy$面的一系列平面上的截面就是J集，在$Ozt$面上的截面就是M集。它的结构是很复杂的，我们不能用球极投影之类的方法来观察它，下面我们先看一下它在其他几个面上的截面：

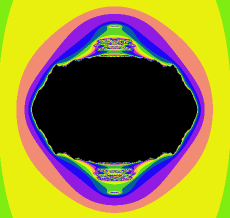
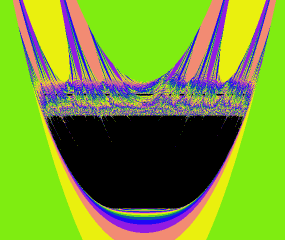
是不是感觉这些都失去了自相似性而很难看？其实，J集和M集有自相似性就是因为那个变换是共形变换，即在变换前后角度大小会不变，直线或圆变换之后也是直线或圆。在不断的迭代中正是由于这种保持形状不变的性质才使得J集和M集的局部和整体相似。在这个四维分形中x和y是相互关联的，z和t是相互关联的，一旦我们从其他面去截就破坏了这种关联，也就破坏了它们的共性性，这样得到的图形虽然也具有无限精细的结构，但没有了自相似性。

我们还可以斜着去截，得到一个M集和J集的“杂合子”：

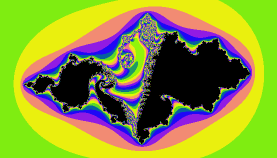
不过这也比较难看，更好的方式是不断改变这个平面的夹角然后看截面动画。由于js不能保存文件到本地，我就没有做这个动画了，大家可以到我那个网页程序上去看。

另外，我们还可以对它作截胞，这样就得到一个三维的分形。真想看一下它是什么样的，但