这是一个奇特的宇宙，它没有边界，但它的体积却是有限的，具有很多神奇的性质。在它里面时你不会发现自己附近的空间与我们的宇宙有什么不一样，但从整体看你就会发现很多异常的地方。从宇宙中的任何一点向任意方向出发最后又会回到这一点，这有点类似于环面，但它和环面又非常不同，它不是环面而是一个三维球面，即超球！所以这是一个弯曲的空间，里面的光线会发生弯曲，形成类似于透镜一样的光学效应。比如你在这个宇宙里面向前看，如果没有障碍物，你会看到自己的头！向前仍一个球，你会看到它先慢慢的远去，速度逐渐变慢，然后居然开始往回走了！当它“回”到你旁边时你伸手去拿，发现它只是个幻影，接着它又会开始远去，并且它变成了倒像！这时你回头看就会看到球从你后面回来了，这次它不是幻影了，而是它在宇宙里面绕了一个大圈后回来的。

同时，这个宇宙也是一个非欧空间，这个宇宙里面的三角形内角和是大于180度的，并且两条“直线”要么重合要么异面。

黎曼宇宙中的科学家们为了让大家更直观的了解它的性质，做了一个很有用的类比：把它类比成二维球面。这样宇宙的结构就直观多了。我们知道，曲面里面的过两点AB间的线段定义为曲面中从A到B最短（或最长）的曲线，这样的直线称为测地线。被限制在曲面中的光以及不受力的物体的轨迹也都是测地线。一个球面上的测地线我们可以很直观的看出就是球面上的大圆，即圆心和球心重合，半径等于球半径的圆。

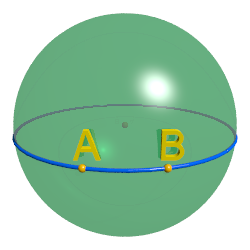
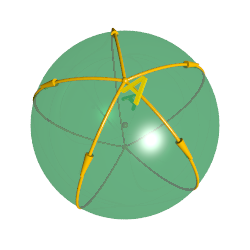
所以科学家们得到了黎曼宇宙中的牛顿第一定律：一个不受力的物体将一直沿半径尽可能大的圆匀速运动，也就是说它会一直在宇宙里面做周期性运动。想象一下，你站在北极处一定会对一个一直在赤道处转圈的物体感到奇怪，其实它的圆运动就相当于我们宇宙中的匀速直线运动！

科学家们对黎曼宇宙中的几何光学尤其感兴趣，因为他们的宇宙是一个“大透镜”，从宇宙里面一点处向四周发出的光线会在宇宙的“另一面”聚焦甚至回到光源处，就像在赤道处有一个凸透镜一样。所以这个宇宙中的任何物体都有两个像，一个是它本身，一个是在宇宙另一面倒立的实像。更神奇的是，你在北极向南极方向仍一个物体，当它到南极附近时就会在北极附近成一个倒立实像。当实像在你眼睛后面时你看到的就是它本身，即一个正立的像，在眼睛前面时看到的就是倒立的像。

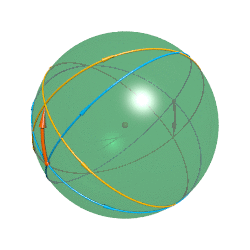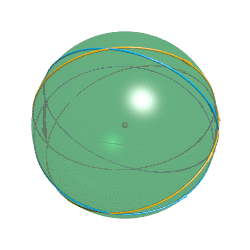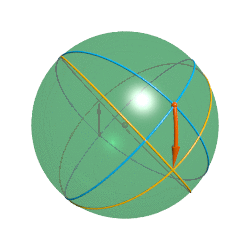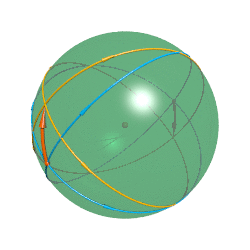
那么为什么物体在从北极到南极的过程中你会看到它先变大再变小呢？既然宇宙和凸透镜都有聚焦的作用，那么它们也具有放大的作用。在一个物体向赤道移动的过程中它向各个方向发出的光在北极附近处时逐渐发散的，所以你看到的像是慢慢变小的；当它过了赤道之后光又开始逐渐聚焦起来，你看到的也就变大了。而它过了南极之后你看到的就是它的倒立实像了。

为了更直观地看出观察到的物体的大小变化，科学家们还根据光路可逆原理发明了一种研究弯曲空间中成像规律的好方法：光线跟踪。既然光线是入射到眼睛里面的，而要想根据空间中的物体找出所有的入射光线是困难的，那我们干脆就从眼睛出发反过去找光线的发出点。假设我们眼睛在北极点处，从北极点发出一簇一定宽度的“光线”，这个宽度就代表视野大小，这样，每条光线最终落到的点就是视野中相应位置看到的点。

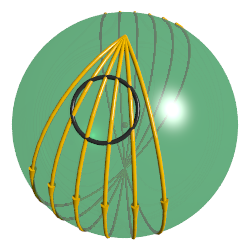
我们发现，一个球在从北极出发向南极运动的过程中，在它到达赤道之前它在视野中的比例是一直变小的，所以我们看到的也就是在变小的，它过了赤道之后比例又开始变大了，当球的前端刚好和南极点重合的时候我们发现从眼睛发出的所有“光线”都落在了球面上的同一点处，那整个视野都被这个点填满了！这时其实就是球被无限放大了，就像我们用放大镜时一样，放大镜离物体越远看到的虚像越大，当这个距离等于聚焦时物体就被无限放大了。不过，虽然是无限放大了，我们也不可能看清的。当球过了南极点后没条光线又和球有了不同的交点，只不过光线在南极点处交叉了一下，之前交点在球最右边的现在到了最左边，相当于整个视野被反过来了，所以此时我们看到的就是球的倒像！因为这时球在宇宙另一面成的倒立实像到了眼睛前面。如果球继续向前运动，我们看到的倒立的球又会经历变小再变大的过程。