我最早也是在physixfan的博客上看到潜水艇悖论的，我觉得它是相对论所有悖论中最难想的了，看似只是狭义相对论，其实要真正解决它用的已经是广义相对论了。

这个悖论是这样的：有一个浮在水里面的潜艇，浮力恰好等于它的重力。那么当它加速时，岸上的人看来潜艇由于尺缩效应长度会变短，密度增大，所以会下沉；而船员在看来却是海水被压缩，密度变大，所以浮力变大了，因此潜艇应该浮起来。他们到底谁是对的呢？

最终的结果是：潜艇会沉下去。那么船员到底错在哪里呢？这个问题的关键就是如何处理重力场。马察斯在他的论文中认为在船员看来，潜艇加速后受到的有效重力将比它加速前受到的大，这个重力增大的效应将大于海水密度增大所产生的浮力，使得潜艇下沉。那么该怎么说明这一点呢？然而坏消息是，重力场已经是属于广义相对论中的了，狭义相对论在重力场中并不成立，所以要真正解决这个悖论只能用广义相对论。

• 用电场类比引力场来试图解释潜水艇悖论
• 广义相对论基础：度规
• 均匀引力场和科里奥利力场的度规
• 均匀引力场的洛伦兹变换
• 费移

假设岸上的人看来空间的重力加速度为$g$，那么潜艇静止时受到的重力和浮力都是$mg$，当潜以速度v运动时根据相对论，它的质量和长度都会发生变化，前者使潜艇的重力变成了$\gamma mg$，后者使浮力变成了${1\over\gamma}mg$，其中$\gamma=1/\sqrt{1-v^2/c^2}$。所以潜艇受到的合力大小为$F_{1}=mg(\gamma-{1\over\gamma})\gt 0$，方向是向下的，很明显潜艇会下沉。

现在我们切换到船员的参考系。为什么在他们的参考系中重力场会增大呢？我们可以先这样定性的解释一下：当潜艇加速时不仅海水被压缩了，重力场也被压缩了，使它的场线变密了，所以潜艇受到的重力就增大了。不过，如果真的是整个重力场增大的话，那海水受到的重力同时也变大了，潜艇还是会下沉，问题到底出在哪里呢？这就是解决整个悖论的关键了，实际上潜艇受到的“有效”重力和海水受到的是不一样的，因为海水相对于重力场是静止的，而潜艇不是！如果我们把这个悖论改一下，改成潜艇不动而海水加速，那么潜艇就会浮起来。这暗示了船员的参考系中还存在一个与物体速度有关的力场！这个力场是磁场的类似物。为了看出这一点，我们把重力场类比成电场。回忆一下电磁场的洛伦兹变换公式：

岸上人的参考系中相当于存在一个非零的电场$E$，在变换到船员的参考系中后这个电场不仅变为了$\gamma E$，而且同时出现了一个大小为$\gamma vE/c$的磁场，我们发现这个磁场的方向使得海水受到的“磁场力”的方向和“电场力”的方向相反！考虑到海水的尺缩效应，并假设阿基米德定律仍然成立，潜艇受到的浮力就是

这个力是大于潜艇受到的浮力$\gamma mE$的，所以潜艇在船员看来也会下沉。问题解决。

然而上面这种类比只是一个“玩具模型”，只能给我们找方向而不能成为推理的依据。不过，我们现在已经知道了一个相对于均匀引力场匀速运动的参考系里面不仅存在均匀引力场，还存在一个类似于磁场的与物体速度有关的力场，我们猜想这是一个科里奥利力场，希望能证明它并把这个力场求出来。由于涉及到引力场了，这就必须使用广义相对论了。我们现在先来介绍一下广义相对论中一个很基础的东西——度规。

度规的定义

我们知道，广义相对论是用弯曲的时空来描述引力场的，一个不受力的物体在时空中的轨迹是测地线，那么怎么描述弯曲时空呢？我们可以用两点间的距离公式来描述，更准确的，是用距离微元，即$(x,y,z)$和$(x + \dd x,y + \dd y,z + \dd z)$间的距离描述。在微分几何中，这样的距离微元就叫做度规[1]。平坦空间中的度规每项的系数都是常数，比如，欧氏空间里面的为$\dd l^2 = \dd x^2 + \dd y^2 + \dd z^2$；闵科夫斯基空间里面的是$\dd s^2 = c^2 \dd t^2 - \dd x^2 - \dd y^2 - \dd z^2$。

那么这个度规呢：$\dd l^2 = x^2 \dd x^2 + \dd y^2 + \dd z^2$？它的$\dd x^2$项的系数是坐标的函数，这是不是代表它表示的空间不是平坦的呢？其实不然。度规是用坐标变量x,y,z等表示的，这说明它是一个与坐标系有关的量，所以我们对它做坐标变换之后得到的是同一个空间的度规。对于上面那个度规，我们只需要做坐标变换$x\to \sqrt{x}$就可以把$\dd x$前面的x消去，所以它表示的仍然是一个平坦空间。而有些空间的度规中也出现了坐标的函数，并且不管我们怎么做坐标变换都不能把它变成常数，比如二维球面

这时候它表示的空间才是非平坦的，即弯曲空间。几何学上有一个专门研究球面上的几何的分支，它就是黎曼几何。

只要我们知道了一个空间的度规就知道了这个空间中的引力场。所以我们需要三样东西：均匀引力场的度规、相对于均匀引力场匀速运动的度规以及科里奥利力场的度规。下面我们一个一个地来。

均匀引力场

我们可以用广义相对论中很有用的一个原理来求均匀引力场的度规：等效原理，即一个匀加速运动的参考系$S'$和一个均匀引力场是等效的。所以我们第一步是要把匀加速运动观察者的轨迹求出来。怎样才是匀加速呢？这里是相对论，可和牛顿力学中的$x=at^2$不一样哦。牛顿力学里面的匀加速是受恒力的物体的运动轨迹，那么相对论中也是一样的，只不过不能用$\vec{F}=m\vec{a}$了，而应该用它在相对论中的推广：

另外，在相对论中我们一般用固有时$\tau$，即运动观察者的时间来作为轨迹参数。它与坐标时t的关系为

当速度v为常数时这个式子就成为我们常见的时间变换公式。 为了计算方便我们设物体是沿z轴方向加速的，这样就不用考虑x和y坐标。把力F当成常数，并设$F=m_0a$，我们就可以得到物体在$S$系中的轨迹方程

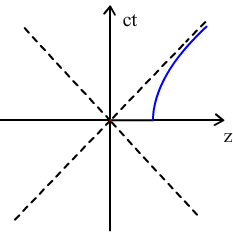
这是一条双曲线，当固有时$\tau$趋于无限大时轨迹无限趋于直线$ct=z$，也就是它的速度会无限趋于光速，这正是我们期待的。虽然它按照牛顿力学定义的加速度并不是常数，但它的固有加速度却就是常数a。由于固有加速度的定义涉及到了广义相对论中的更多内容，这里我就不介绍了。

下一步我们需要求出以这个匀加速观察者为参考系的度规。首先我们需要找出坐标变换关系。我们可以通过这种方法来求：设在原坐标系中的一点$B(ct,z)$，然后在轨迹上找到一点$A(ct',z')$使得矢量$\vec{AB}$与轨迹在A处的切矢量$\vec{t}$正交（注意，是闵科夫斯基时空中的正交，即$t_{1}t_{2}-z_{1}z_{2}=0$），这样观察者A观察到的B的时间坐标就是A点处的轨迹参数$\tau$，x坐标就是$\vec{AB}$在A点处轨迹的单位法矢量$\vec{n}$上的投影。

为什么这样做就是对的呢？其实根据相对论直线AB就是观察者A的同时线，所以B的时间就等于A的时间，即固有时$\tau$，这就相当于A点处的切线是时间轴，法线是x轴一样，这个坐标系叫做观察者A的固有坐标系。在更高维的时空中直线AB就会成为一个面甚至是胞，我们只需要在这个空间里面选取几个相互正交的基矢量就可以求出空间坐标。如果时空不是平坦的，只需要把直线AB换成AB之间的测地线，把$\vec{AB}$换成测地线在A处的切线。

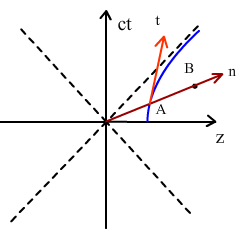
下面我们把这个方法应用到匀加速观察者上。先找出轨迹上任意一点A的切矢量和法矢量。幸运的是，法矢量的所在直线是过原点的！这大大简化了计算，我们方程都不用列就可以写出$A(ct',z')$和$B(ct,z)$的坐标变换关系了：

这样度规就是

在重力场中，根据等效原理，相对于一个加速度为g的参考系。所以重力场的度规就是把上式中的a换成g即可。 重力场的度规有一个很有意思的性质：当$z=-a/c^2$时它$\dd t$项的系数就为0了。如果我们根据上面的坐标变换关系画出重力场中的测地线就会发现所有的测地线都是以这条直线为渐近线的，即物体不能穿透这条直线。这其实很有道理，重力场是恒引力场，引力场会弯曲光线，所以如果某个点离原点处的观察者足够远那这点处发出的光也无法到达观察者。

相对于均匀引力场匀速运动的参考系

我们已经得到了岸上的人的参考系度规，下一步就是求出船员的参考系的度规。这是很关键的一步，因为这个度规里面就存在科里奥利力场的成分了。我们设有一个在重力场中沿x轴以速度v运动的观察者，那么它的轨迹方程就应该是

同样地，我们先求出坐标变换公式。如果要直接在重力场中求就会很麻烦，因为空间中的测地线不是直线。所以我们还是选择使用等效原理，即先求出这个观察者在$S$系中“平抛运动”轨迹。这很容易做到，只需把上式代入之前那个坐标变换公式：

这里由于等效原理我们已经把加速度a换成了g。然后再利用上面讲的那个方法求。然而此时由于时空变成了三维时空，在求空间坐标时就涉及到两个法矢量。虽然其中一个很简单，在x方向上的分量为0，但另一个就很一般了，只能硬着头皮去解方程。我去年算了很久才算出来，但就只发现引力场强度变大了，并没有发现科里奥利力场。上个星期我重新用Mathematica算了一下，发现我去年算的是错的！科里奥利力场使度规变得很复杂，我开始都怀疑是我方程打错了。Mathematica计算的结果是：

这个度规中$\dd t$的系数的第一项和均匀引力场度规很相似，只是把g换成了$1/(1-v^2/c^2)g$，这代表的就是变大了的均匀引力场。剩下的那些复杂的项代表的就是科里奥利力场。是不是感觉很不直观？为了让它看起来更直观一点，我们还需要求出科里奥利力场的度规来和它对比。

科里奥利力场的度规

这个度规的求解就很简单了。设角速度的方向是沿y轴正向的，大小为$\Omega$，那么我们立即就可以写出坐标变换关系：

所以度规就是

说是科里奥利力场，其实是科里奥利力场和离心力的合力场。只不过在a和v不是很大的时候离心力可以忽略。

问题完美解决

现在对比这个科里奥利力场的度规和上面那个度规，我们可以看出$\Omega = gv / (c^2-v^2)$。我们有必要关心一下角速度的方向，只需注意到科里奥利力场的度规和上面那个度规之间出现角速度的项是一致的，只是符号不一样，所以角速度是沿y轴负方向的，海水受到的科里奥利力的方向是沿z轴正向的，与它受到的重力方向相反。 另外均匀引力场的大小为$g/(1-v^2/c^2)$。这里必须说一下，引力场是不满足叠加原理的，虽然度规看起来是这两个场的叠加但是严格的讲它并不是科里奥利力场和均匀引力场的叠加。不过在g和v不是很大的情况下叠加原理还是近似成立的，所以海水的受力就是科里奥利力和引力的叠加。

假设潜艇在加速前重力和浮力都为$mg$，那么加速后受到的重力为

我们仍然认为阿基米德定律没有错，所以浮力就等于排开的水的重力，它等于重力减去科里奥利力。海水受到的重力和科里奥利力分别为

所以海水受到的有效重力，也就是浮力大小，为

这样，潜艇受到的合力就是

所以重力是大于浮力的，潜艇仍然会下沉，问题解决！ 其实当我们得出那个相对于均匀引力场匀速运动的度规时我们已经可以用4加速度直接算出海水和潜艇的受力大小了，而且算出来的还不是近似值。只不过那也涉及到更深的广义相对论了，而且恐怕也只有交给Mathematica算，为了简单直观我就做了一个近似处理。马察斯在他的论文里面提到了Supplee在之前用纯狭义相对论的方法得出的近似结果，和我差了一个系数2，暂时我还没找到原因。我想如果我直接用度规算那应该和得到和马察斯差不多的结果。

现在我们思考一下为什么在均匀引力场里面加速会出现科里奥利力场。科里奥利力场产生的原因就是观察者的旋转，所以相对于均匀引力场匀速运动的观察者同时也在“旋转”！准确的说，是观察者没有沿自己的轨迹费移，也就是在相对论中他其实是在一边旋转一边平移的，这就产生了科里奥利力场。

[[1]]:很多物理书上都把另外一种量$g^{\mu\nu}$称为度规，而把我们这里说的度规叫做线元。这只是一种通俗的说法，在微分几何里面$\dd s^2$就是度规本身。详见《微分几何入门与广义相对论》45页，选读[[2-5-2]]。