四维几何学 6-超球外翻
球面外翻问题是拓扑学中的一个很有趣的问题:把一个球面的内侧翻出来,你可以随意拉扯、变形甚至使它自相交,但是你不能把球面撕开或者强行把一个尖角拉成平的。这看起来是不可能的,但实际上这不仅可以做到,而且还存在多种解法。这是对空间想象能力的大挑战,你能想出一种解法吗?这个视频里面详细地讲了一种比较容易理解的方法,看了之后你基本上就懂了。

好,我们现在再次挑战想象力:你能把超球()同样的把内侧翻到外侧来吗?你也许被这个问题惊呆了,球面的外翻都那么复杂,超球根本就没法想象了。不过,其实这个问题并没有想象中的那么难。
旋转数(Turning number)
这部分内容都出自上面的视频,建议大家先去看一下。
和所有的数学问题一样,我们要先证明一个想法是否可行,然后再谈具体怎么做。为了证明不同维度中的球面是否可以外翻,视频中讲了一个很重要的概念——旋转数,它是封闭曲线、曲面以及四维空间中的曲胞在按照我们的规则变换时保持不变的一个量。视频中还讲了旋转数的一种简单的计算方法,为了能推广到其他维,我这样叙述它:先要找出这个封闭图形上所有法线方向为一个特定方向的点,然后把这些点的数量相互加减,具体怎么加减,这在不同维的空间中是不一样的,必须要使得这样得出的数是一个不变量。在下面的讨论中我们选择这个“特定的方向”为向上的方向。
二维空间中曲线上存在两种法线向上的点:上凸点(视频中称为“笑脸”)和下凹点(视频中称为“哭脸”),它们总是会成对出现或消失,所以它们的个数差就是二维空间中的旋转数。如果我们真的把一个旋转数为1的圆外翻了,那么它上面的法线就反向了,旋转数就成了-1,与原来的不相等。这就是圆不能外翻的原因。
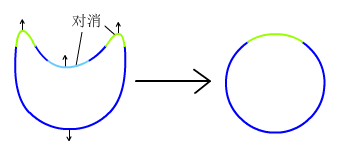
这个计算方式不能直接推广到三维空间中,因为三维空间中的曲面的“峰”和“盆地”不能像二维空间曲线的上凸点和下凹点那样对消,相反,曲面上还存在一种法矢量向上的点——鞍点(山谷)。鞍点既可以和峰对消又可以和盆地对消,所以三维空间中曲面的旋转数应该是峰加上盆地再减去鞍点的个数。这样不管球面是那个面在外面它的旋转数都是1,所以球面是可以外翻的。
既然二维空间中的圆不能外翻,三维空间中的球面可以外翻,这就暗示了只有奇数维中的球才可以外翻,即超球可能根本就不能外翻!真的是这样的吗?下面我们继续讨论。
四维情形
当我看到视频中的旋转数定义时,我马上就在想四维空间的旋转数该怎么办?为了解决这个问题,我们要先找到四维曲胞上法线向上的点。我们知道如果我们画出三维曲面的等高线,那么在峰和盆地附近等高线会成一个个的圆,峰周围都是高度减小的方向,盆地周围高度都是增加的;在山谷周围等高线成一个X形,周围的两个方向中一个方向是高度增大的方向,另一个是减小的方向。
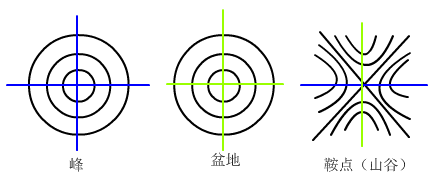
其中蓝色线代表高度减小的方向,红色代表增加。为了把三维情形类比到四维空间中,我们画出曲胞的“等高面”。这样类比出来的等高面有两种:一种是一簇同心球,另一种是一簇圆锥面和双曲面。
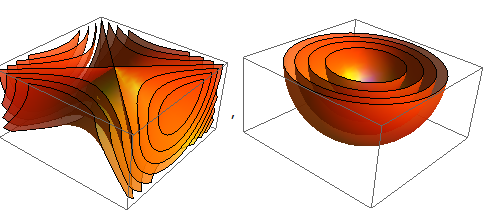
这其实就是上一篇文章里面讲的两种四维等高面!它们分别是旋转抛物面和旋转双曲抛物面的等高面。
那么曲胞上就只有这两种法线向上的点吗?不是的,我们还没考虑它们附近的高度变化情况。由于现在这些点周围都3个方向,所以高度的变化趋势就会有4种组合:升升升、升升降、升降降、降降降。我也不知道怎么给它们取名字,下面的讨论中我们干脆分别就叫它们A,B,C,D好了。
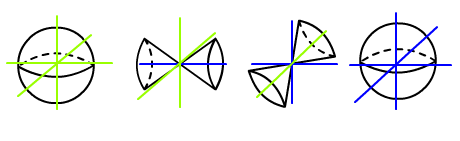
现在我们知道了四维空间中的曲胞上的四种点,下一步就是讨论旋转数是这些点怎么加减得到的了。就像视频里面说的一样,虽然超球没有B和C,但是关键是这些点的相互作用。
对消律
和三维空间类似,我们需要找出A,B,C,D中哪些组合可以对消,哪些不能。为了找出可以对消的组合满足的条件,我们先来讨论为什么峰和鞍点可以对消而峰和盆地不行。
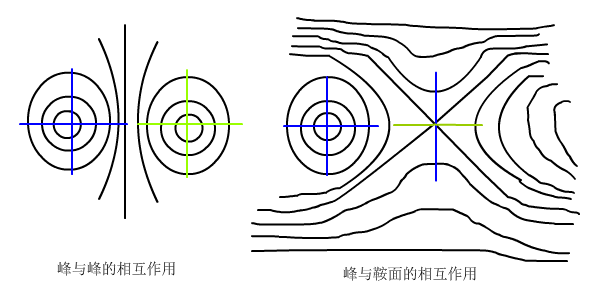
鞍点和峰之所以可以靠近并对消是因为它们只有一个方向上的高度变化趋势是不同的,另一个变化趋势相同的方向在它们靠近时就会相互“匹配”,这使得平行于它们靠近方向上的等高线在两边都是沿一个方向的(如上图),当它们对消后就只留下上面这些等高线。而峰与峰靠近时垂直于它们靠近方向上不同的高度变化趋势就会阻止它们靠近,等高线也不能统一,也就不能对消。
在其他维空间也是类似,只要变化趋势不匹配就不能对消。所以两个法线向上的点可以直接对消的条件就是它们有且仅有一个方向上的高度变化趋势不同。 所以曲胞上那四种点能直接对消的组合有:
- A与B
- B与C
- C与D
其中第一个和第三个相互靠近时的等高面很容易想:就是峰与鞍点靠近时的等高线的旋转曲面。第二个就有点难想了,在两点处的等高面是两个对称轴相互垂直的圆锥面,它们之间的部分就不好想了。不过它们还是可以对消。
能相互对消的就只有这三对吗?不是的,A与D可以间接地对消!为什么呢?既然B和C可以对消,那么我就可以产生一对B和C,然后让B和A对消,C和D对消。这是很关键的一点。
知道了对消律,我们就可以写出四维空间中的曲胞的旋转数计算公式了。A和C中的任意一个都可以与B和D中的任意一个对消,所以要使得旋转数是一个不变量,它的计算公式应该是:
好了,现在我们再来用这个公式证明超球外翻的可行性。一个超球有一个A,旋转数为1,把它外翻之后它就变为了有一个D,旋转数也变成了-1,这两个旋转数不相等,因此我们前面的猜想是对的:超球不能外翻!这也许是个好消息,我们不用费尽心思的去想超球怎么外翻了,毕竟四维本身就比较抽象。
在n维中的推广
在看了四维空间旋转数的计算公式之后大家应该都可以找到规律了吧?在n维空间中的超曲面上法矢量向上的点一共有n种,第k种点周围高度的变化趋势有k个方向高度是减小的,(n-k)个方向是增大的。我们按高度减小方向的个数把这些点这样排列:
上面相邻的两种点可以直接对消,因为它们只有一个方向不一样。间隔奇数种点的两种点之间可以间接对消,比如第一种可以和第二种直接对消,和第4,6,8,...种间接对消。也就是说,第1,3,5,...种中的任意一个可以和第2,4,6种中的任意一个相互对消。所以n维空间超曲面的旋转数就是第1,3,5,...种点的个数的和减去第2,4,6种点的个数。
高斯曲率
我们上面这种通过“对消律”来得出旋转数计算公式的方法虽然也得出了正确结论,但这是凭直觉得出来的,很不严密,我们需要旋转数的准确定义,而不是用几个ABCD的加减来定义。在数学上n维空间中封闭超曲面的旋转数是通过曲面的总曲率除以这个空间单位超球的表超面积定义的。总曲率就是曲面上各个点的[高斯曲率](https://en.wikipedia.org/wiki/Gaussian_curvature)对曲面的积分:
其中就是超曲面上的超面积元,是n维单位超球的面积,它可以用一种巧妙的方法可以得到:
这个方法出自peskin的An introduction to Quantum field theory,在维度正规化部分讲的。首先根据高斯积分公式我们知道
两边同时取n次方,我们得到
上面的就是我们想要的,所以
用这个公式我们可以直接得出只有奇数维中的球才可以外翻的结论,只需注意到一般可以写成的形式,当我们把球外翻之后每个都变成了这样新的旋转数就等于原来的乘以,所以只有n为奇数的时候旋转数才不会变。
对消律的根源其实就是高斯曲率。三维空间中的峰和盆地点的高斯曲率都是正的,而鞍点的为负的,所以它们在积分的时候就会相互抵消。同样,四维空间中的A和C高斯曲率为正,B和D的高斯曲率为负。为什么高斯曲率为正的盆地类比到四维空间中就变成负的了呢?这来源于高斯曲率的定义。
高斯曲率是一个曲面在某个点处的内在曲率,也就是说它的大小与坐标系的取法无关。一条曲线的高斯曲率就是根据二阶导数算出来的那个曲率,曲面的高斯曲率定义为两个曲率的积,这两个曲率分别是过这个点的曲面法线的平面与这个曲面的交线在这一点处的曲率的最大值与最小值。说的有点绕,举个例子可能要好点。对于在二维空间中一个半径为r的圆,它上面的任意一点的法线方向都是沿半径向外的,所以平面与球的交线始终是一个半径为r的圆,最大和最小曲率都是,因此球上任何一点处的高斯曲率都是。单位球的表面积,所以球的旋转数为
对于峰,它周围两个方向都是高度减小的方向,所以最大和最小曲率都是负的(因为平面与它的交线是上凸的),对于盆地最大和最小曲率都是正的,所以它们的高斯曲率都是正的,而鞍面由于有一个方向高度增大,另一个方向高度减小,所以曲率是一正一负的,它的高斯曲率就是负的。
如果把高斯曲率类比到四维空间,它就应该是三个曲率的积,根据它们周围高度的变换趋势,有奇数个减小方向的,即B和D,就会得到负的高斯曲率。剩下的A和C就是正的。
思考题
还记得环面的两个四维类比,环球和球环吗?请用旋转数说明它们可不可以外翻。
上次的答案: 南极处的所有轨迹都相互重合,即一个圆,北极的轨迹也都是重合的,只不过是一条直线,即半径为无穷大的圆。