量子隧穿是一种很神奇的现象。根据量子力学，万物都有波动性，这就导致了一个很反常的现象：就算物体的能量不足以穿过某个障碍物它仍然有一定的几率穿过这个障碍物。举个例子，停在车库中的一辆汽车是有可能穿透车库门跑出来的！只要你等的时间足够长。不过，实际上只有微观粒子，特别是电子，隧穿现象才很明显，就算你加一个电场把电子束缚住它也有几率会漏出来，当然，电场越强几率越小。而像汽车这种宏观物体，这个“足够长”已经大于宇宙年龄了。。。因此你完全不用担心你车库里面的汽车会跑出来。

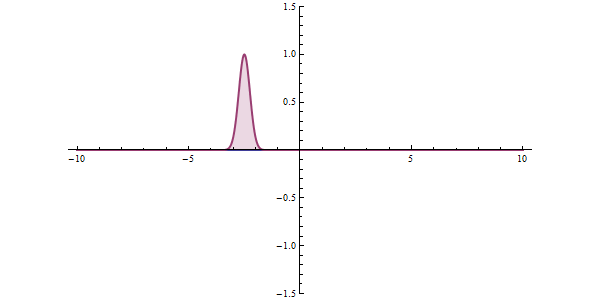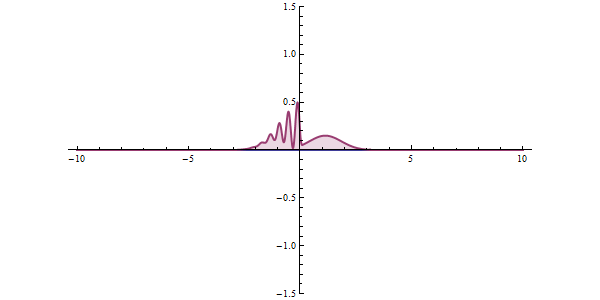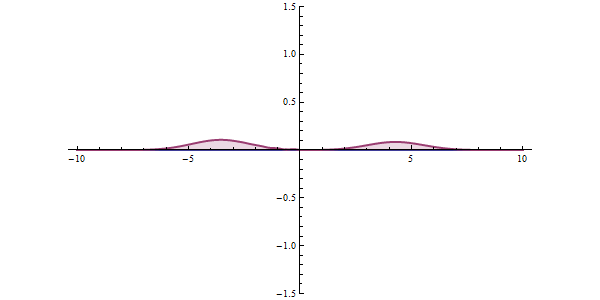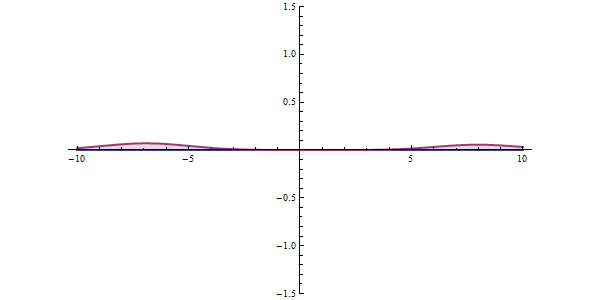
在量子隧穿中还有一类很神奇的现象：共振隧穿。它就跟共振一样，当粒子的能量取某些值时隧穿的概率会突然增大以至于接近1，就像根本就没有障碍物一样！当能量稍微再增大一点时概率又会迅速下降。这是怎么做到的呢？下面我们来讨论一下。

下面我们看到的就是一个电子隧穿时的波函数，中间的白色部分就是“障碍物”。它在“碰”到障碍物时分裂成了两部分，较亮那部分的振幅就是它被反射回来的概率，较暗的另一部分呢？那对应它发生隧穿的概率。

中间的障碍物一般可以用一个势垒表示。什么是势垒呢？可以把它想象成一个具有一定高度的墙，这个高度就是它的能量，在经典力学中粒子的能量必须要大于它才可以越过它，不然就会被弹回来，在量子力学中就算粒子能量小于势垒它也有几率穿过去，这就好像在势垒的下面打了一个隧道一样，粒子的波函数只是振幅减小了。

这种只有一个势垒的隧穿就叫单势垒隧穿，粒子的能量越高或者势垒的宽度越小那么隧穿的概率就越高。取不同的势垒高度画出来的隧穿几率与粒子能量的关系是这样的：

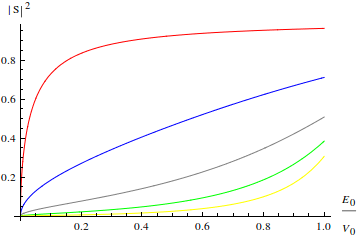
很明显，势垒越窄曲线上升地越快，即粒子更有可能发生隧穿。

上面我们看到的都是单势垒隧穿，那么如果有两个势垒呢？可以这样想：粒子在穿过第一个势垒后有可能在两个势垒之间来回反射，由于粒子也是波，所以如果粒子的能量恰好使这些来回反射的粒子波叠加后相互加强，这就会使得在两个势垒之间的波函数的振幅变得很大，隧穿几率也会很大；相应的，如果这些波相互抵消那么隧穿几率就会很小。这种隧穿几率增大的现象叫做共振隧穿。它和一根管子里面的声波很类似，当管子的长度等于声波波长的整数倍时波相互加强形成驻波，听到的声音最大。我们先来看一下一个波包的隧穿共振动画：

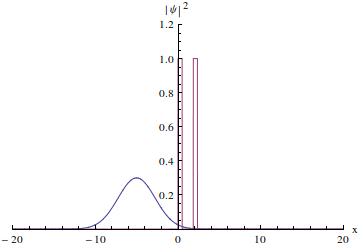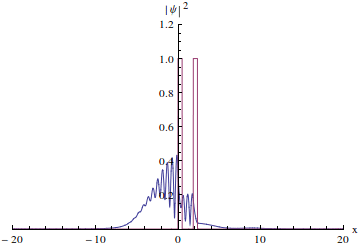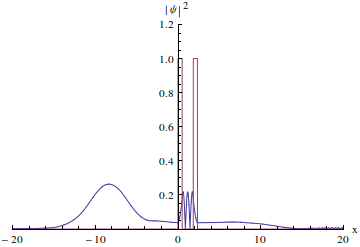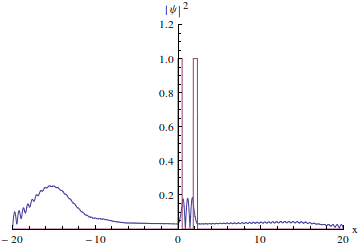
虽然还是只有很小的一部分波函数穿过去了，但请注意：当波包离开时两个势垒周围的波函数值仍然保持不为0的状态，势垒两边“残留”的波函数基本上相等，而且没有要减小的意思，所以，共振隧穿已经发生的。只不过波包是一种“不纯”的波函数，它是很多个具有不同能量的波函数叠加成的，当它穿过双势垒时它里面具有某种特定能量的波函数成分会顺利通过双势垒，其他的隧穿几率就很小，会被反射回去。所以双势垒也是波函数的“滤波器”。

下面我们画出一个波函数很“纯”的粒子发生共振隧穿时的图像，我们发现在两个势垒之间的振幅非常大（红色的线是势垒）：

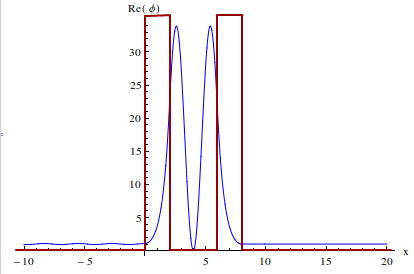
这个图像是不是和上面波包离开后的图像很像？我们发现入射的振幅和穿透过去的振幅基本上一样，也就是说粒子毫无阻拦地过了两个势垒，好像两个势垒根本就不存在一样！

我们可以把双势垒隧穿看成是两个单势垒隧穿，虽然粒子穿过第一个势垒的几率不大，但是穿过的波函数会在两个势垒之间不断反射，振幅越来越大，从而使得它穿过第二个势垒之后的振幅也越来越大，达到稳定时这个振幅就和入射时的振幅差不多了。

同样的，我们画出隧穿概率与能量的关系，得到的图像和上面的单势垒隧穿大不一样：

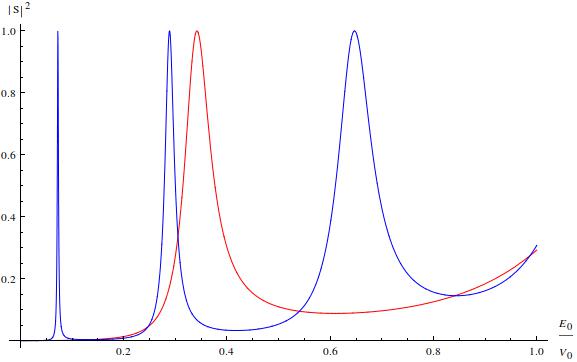
曲线不再是单调递增的了，而是存在几个峰，并且峰值都是1，它们就对应发生共振隧穿时的能量大小。这些峰有宽有窄，越窄说明这个能量值处的共振隧穿对波包能量的选择性越高，这和滤波器的频幅特征是类似的。比如上面动画中那个能量值的峰就比较窄，所以大部分的波包还是被反射回来了。

图中的两条曲线的势垒间距就是不同的，蓝色曲线的较大。这其实很正常，因为间距约等于粒子波长的整数倍时共振就会发生。如果我们继续增大间距，就会得到更多的峰，所有的峰值都是1，靠近纵轴的峰会非常细，所以对波包的选择性更强。

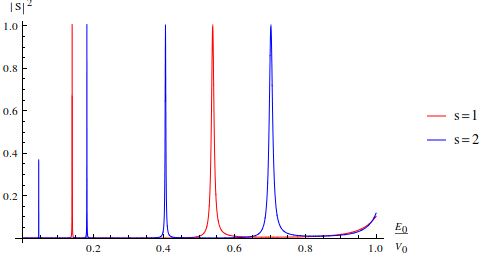
本来我想求出隧穿几率与粒子能量的关系的，但计算实在太复杂了，就是最简单的方势垒情形Mathematica算出来都是一大篇，所以我只能求几个数值解。。。

我第一次看到共振隧穿时第一反应就是：它也许可以用来实现超导。但遗憾的是，我们上面也看到了，只有能量（或者说动量）为特定的几个值时共振隧穿才明显，所以只有当电流为特定值时才会出现这种现象。不过，虽然共振隧穿不能实现超导，但它却有其他用处，比如广泛用于微波电路中的隧道二极管，它里面就有一个三势垒。其实不仅仅是双势垒存在共振隧穿现象，多势垒也存在。在隧道二极管中当电压为某个值时电流中的电子就会发生隧穿，此时电流达到一个极大值，当电压稍微增大一点时共振状态被破坏，电流于是开始下降，这就导致了在一定范围内电流随着电压的升高而减小的神奇现象！这样它的伏安特性就是一条S形曲线，电流随着电压的升高而减小的区域就称为负阻区。