四维几何学 4-解析几何
在这篇文章中我们将讨论一下四维空间中的解析几何。
说是解析几何,其实并没有高中那种繁复的计算。我们会把三维空间中的各种直线平面以及二次曲面方程推广到四维空间,并着重分析四维空间中二次方程表示的曲胞。
重点内容
- 四维空间中直线、面、胞的方程
- 二次曲面:双曲面、双曲抛物面、旋转抛物面的四维类比
- 各种二次型方程对应的曲胞以及它们的截胞
一次方程
和三维空间一样,我们来讨论一下四维空间中直线、面、当然,还有胞的方程。
直线方程和胞方程都比较简单,直线可以类比三维空间的,胞由于有法向量,所以可以类比三维的平面方程。关键是平面方程,四维的平面没有法向量,不能直接类比。
- 参数方程 最容易想到的应该是参数式方程,如果有两个在面中而且不平行的矢量,那么面中发的任何一个矢量都可是表示成,只要我们再知道平面过的任何一点的坐标,就可以写出它的参数方程。
- 点法式方程 虽然四维中的平面没有法矢量,但它有法平面,即与它绝对垂直的平面。一个平面的“方向矢量”可以用2-矢量(可以先看一下这里还有这里)来表示。所以,对于一个法2-矢量为的平面,任何一个矢量在面中的条件就是它与法2-矢量正交,即满足,在加上面中一点的坐标就可以写出完整的方程。注意上面2-矢量与矢量间的张量内积的结果依然是矢量,所以点法式方程写出来会有4个。
- 交胞式方程 上一篇文章中我们说到过两个胞可以交于一个平面,我们也就可以把平面方程写成两个胞方程的方程组的形式,即
但这是很不直观的,立体几何里面我们也很少用直线的交面式方程。类似于三维空间,我们也可以把这种方程转化为点法式方程。从上面两个方程我们可以看出两个胞的法矢量分别为,把它们做楔积就得到法2-矢量,然后再随便求出平面中一个点的坐标就可以了。
二次方程
下面的就比较考想象力了,我们来看一下四维空间中各种二次型方程对应的图形。这里由于这些几何体都不能进行球极投影,截面法反而用的要多一些。 由于下面的分析中经常用到旋转变换,所以这里先简单说一下四维的旋转。在三维中我们常说绕什么轴旋转,但其实只有在三维空间中才能说绕轴旋转(原因看这里),更具有一般性的说法是在什么面中旋转,如绕三维中的绕z轴旋转就是在xy面中旋转。在下面的讨论中我们就会使用这种说法。
- 这个一看就知道是四维空间中的球面,即三维球面,我们把它称为超球。它的四视图都是半径为的球,当它穿过三维空间时我们看到一个球慢慢变大,然后变小,最后消失。
- 这个方程不外乎就是在上面那个的基础上做了伸缩变换,把超球在四个方向上拉伸过了,成了一个超椭球。我们把它叫做四轴超椭球,它的截面是三轴椭球。
- 现在我们改一个符号,得到的方程又代表什么呢?如果,那么当取不同的值时就得到半径为的球,也就是说如果用t等于常数的胞去截它,那么从开始往上走我们就会看到一个球,它的半径均匀变大。其实这就是圆锥的一种类比——球锥,其实就是相对论中说的光锥。如果我们从它的侧面去截,就会看到一个双叶双曲面慢慢变成圆锥面,此时我们看到的就是它的“母面”,之后又变成双叶双曲面。那如果斜着截呢?这可能有点难想了,事实上,我们会得到旋转椭球以及双曲面,还有,当我们的截胞垂直于它的任何一个“母面”时我们就会得到旋转抛物面。是不是感觉这三个东西有点熟悉?是的,我们截球锥就会得到圆锥曲线的旋转面! 既然我们已经知道了时是圆锥的类比,那么当以及时分别得到单叶双曲面和双叶双曲面的类比。三者都是轴对称的,都是球扫出来的柱胞,只是球体半径在扫的过程中变化不一样。我们把它们统称为旋转双曲胞。我猜想它们也可以通过类比下面这种把圆柱扭成双曲面的过程得到:
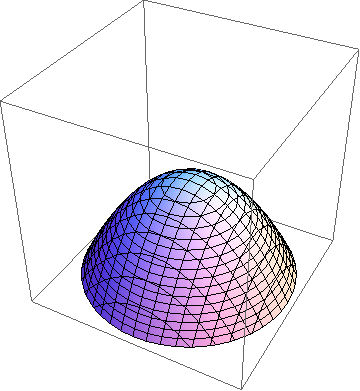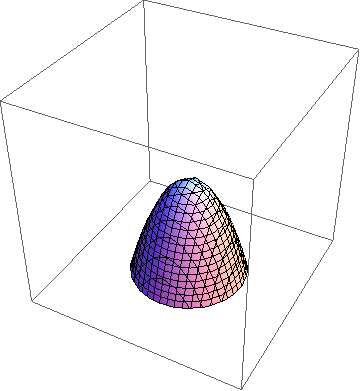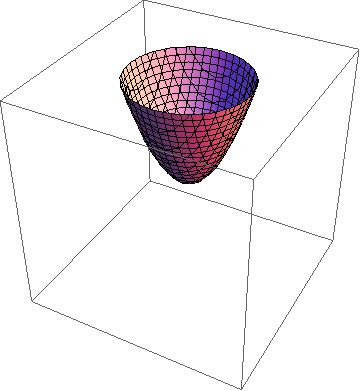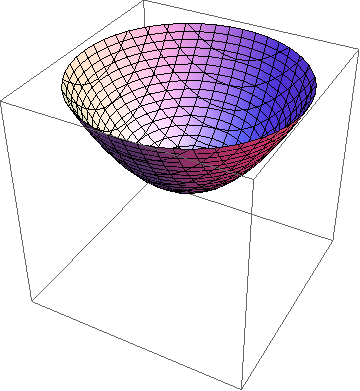
斜着截球锥时得到的抛物面 四维球柱的底面是一个球,我们也许可以类似地扭动这个球来把它的侧胞扭成双曲的。但由于球胞的侧胞是展不开的所以这个猜想可能不对。 既然知道了表示的曲胞也就不难知道所表示的东西了吧,只是做了一个伸缩变换而已。
扭动圆柱得到双曲面 - 我把这个曲胞叫做双曲胞,你马上就会问它和上面的旋转双曲胞有什么不一样呢?我们先来看的情况。我们发现方程变成了,好像是两个距离相等。我们知道面和面是绝对垂直的,所以等式两边分别是到面和面的距离,所以方程描述的就是到这两个面距离相等的点的集合。这是一个什么图形呢?在三维空间里面我们知道到两条异面直线距离相等的点构成双曲抛物面,即马鞍面。我们猜想这个图形可能是马鞍面的某种类比。 不管从xyzt中的那个方向去做截胞,得到的都是一样的!即一个单叶双曲面慢慢变成圆锥面,然后又变回单叶双曲面。然而这样我们还是不容易对它产生直观的感觉,我们再来看一下它的斜截胞: 我们果然得到一个变化的马鞍面,而当截胞向远处移动时截胞趋于一个平面!然而这样它还是很抽象,我们需要分析一下方程。 我们发现这个方程不外乎是把双曲面方程中的换成了,所以双曲胞就是双曲面的旋转胞!即它是三维双曲面的另一种类比,只是旋转所在的面不一样。得到双曲胞所在的旋转面只能是,与截胞所在胞的交线就是z轴;得到旋转双曲胞的旋转面是,其实任何一个过t轴且垂直于z轴的面都可以,因此它具有更高的对称性。如果不把它们放在坐标系中,你能说出怎么得到这两个四维曲胞吗?
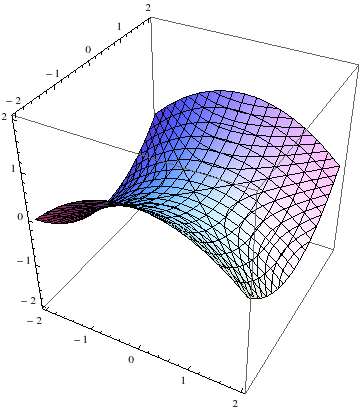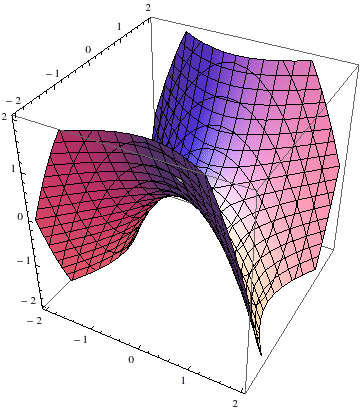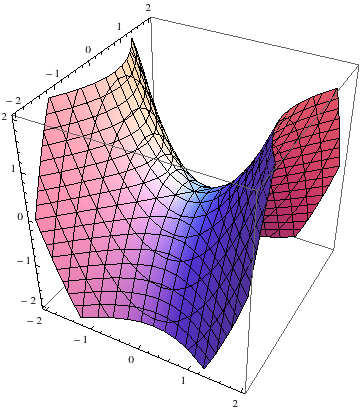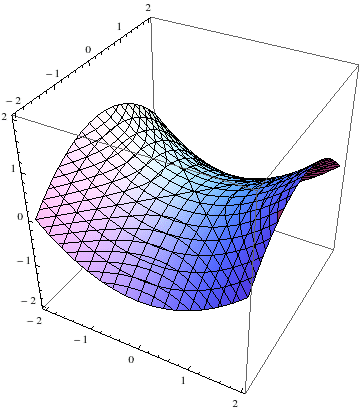
双曲胞的斜截胞
下面我们来讨论包含一个一次项的方程,我们只需要讨论两种,因为其余的都是这两种旋转或者镜像出来的。我们把一次项都设为t,并把它看成“高度”,那么方程就可以看成一种高度函数,这时我们令得到的截胞就类似于地理里面用于描述地形的等高线图,只不过这个“线”变成了面。地理中我们知道地形的基本元素是山峰、山谷和盆地,四维的地形也有相应的类比,下面我们就来看一下“四维地形学”。
- 这个方程对应的曲胞我们称为旋转抛物胞,是四维“山”的“盆地”,因为xyz都是“高度”t增大的方向。如果我们把t反个号就得到“山峰”,这时三个方向就都是“高度”减小的方向。 从t轴方向去截它就得到一个半径在变化的球,从侧面截就得到旋转抛物面。并且它是旋转抛物面在任意一个过t轴且垂直于它对称轴的面中旋转得到的曲胞。
- 这个又有点抽象了,它是马鞍面的类比,我们把它称为旋转双曲抛物胞,是四维“山”的“山谷”。我们知道三维的山谷是沿某个方向(如x)是高度增大的方向,另一个垂直的方向(如y)是减小的方向。而在四维中反而有点对称破缺,沿x和y这两个方向是t增大,z则是t减小的方向。同样的,如果把t反号,那么就是两个减小,一个增大。 从方程来看它是把中的换成了(注意此时y成了第四维),所以它可以看成是马鞍面在中旋转成的曲胞,x轴方向恰好就是马鞍面上升地最快的方向。
下一篇文章我们就会用到这两种四维“基本地形”。
思考题
请找出环面(即甜甜圈形)的四维类比并想出截面动画。你会发现如果用解析法会更容易得出答案,但缺乏直观性。
上次的答案: 类比三维空间可以知道16胞体相邻两个胞的法向量分别为以及,所以夹角余弦值为
由于这两个法向量都是指向多胞体外部的,所以其实是夹角的补角,真正的应该夹角为.