我们知道，几何学就是一个建立在有限个公理上的理论体系，公理推出一系列定理，然后定理再继续推导出定理。所以在这篇文章中我们将像立体几何那样给出四维空间的公理、定义以及一些定理，并给出证明．大家在看证明之前可以先自己思考一下证明过程． 在下面的证明中我们小写希腊字母或多个拉丁字母表示面，用大写希腊字母表示胞． 证明中会出现较多几何语言，大多都和立体几何的类似．

这篇文章会长期更新，如果我想到了一些新的定理就会把它补充进来．

• 各个四维位置关系的准确定义
• 判定定理及证明
• 二面射影面积定理的证明

• 公理1：三条共点且两两不平行不共面的直线可以确定一个胞．
• 公理2：两个交于直线的面可以确定一个胞．

这些公理我们看起来也许并不是公理，但在四维生物看来却很显然，就跟我们觉得三点确定平面一样自然．

下面是四维空间中新元素之间位置关系的准确几何定义，大多数是通过类比得到的，最大的不同在于二面角．

• 线胞平行：如果直线$l$和胞$\Gamma$没有公共点，且这条直线可以通过平移包含于这个胞，那么这条直线就平行于这个胞，记为$l\parallel\Gamma$
• 线胞垂直：如果直线$l$垂直于胞$\Gamma$中的所有直线，那么$l$就垂直于这个胞，记为$l\bot\Gamma$．
• 线胞角大小：直线$l$与胞$\Gamma$的夹角大小为$l$与它在胞$\Gamma$中的射影的夹角大小．
• 面胞平行：如果面$\alpha$和胞$\Gamma$没有公共点，且可以通过平移包含于胞$\Gamma$，那么这个面就平行于这个胞，记为$\alpha\parallel\Gamma$．
• 面胞角大小：面$\alpha$与胞$\Gamma$的夹角大小为面$\alpha$中的直线与胞$\Gamma$夹角的最大值．
• 面胞垂直：如果面$\alpha$与胞$\Gamma$的面胞角为90度，那么它们就垂直，记为$\alpha\bot\Gamma$．
• 二胞平行：如果胞$\Gamma$中的所有直线都平行于胞$\Delta$，那么这两个胞就平行，记为$\Gamma\parallel\Delta$．
• 二胞角大小：胞$\Gamma$与胞$\Delta$的夹角大小为胞$\Gamma$中的直线与胞$\Delta$中直线夹角的最大值．
• 二胞垂直：如果胞$\Gamma$与胞$\Delta$的夹角大小为90度，那么它们垂直，记为$\Gamma\bot\Delta$．
• 线面平行：如果一条直线可以通过平移包含于一个平面，那么它们相互平行．
• 线面垂直、线面角：定义同三维空间，如果不共胞就先把它们平移至共胞．
• 二面角大小：面$\alpha$与$\beta$所夹二面角大小记为二元组$(\theta_{1},\theta_{2})$，其中$\theta_{1}$与$\theta_{2}$分别为$\alpha$中直线与$\beta$夹角的最大值与最小值．记为$\langle\alpha,\beta\rangle=(\theta_{1},\theta_{2})$．
• 二面平行：同三维空间．
• 二面半垂直：如果平面$\alpha$中的某一条直线垂直于平面$\beta$中的所有直线，那么这两个平面半垂直，记为$\alpha\bot\beta$．
• 二面绝对垂直：如果两个平面$\alpha$和$\beta$中的任意两条直线都相互垂直，那么这两个平面绝对垂直，记为$\alpha\top\beta$．

• 定理1-线胞平行判定：如果直线$l$平行于$\Gamma$中的直线$m$，且$l$在$\Gamma$外，那么$l\parallel\Gamma$． 证明：我们可以把$l$平移使其与$m$重合，这样就满足平行的定义了．证毕．
• 定理2-线胞垂直判定：如果直线$l$垂直于胞$\Gamma$中的三条不共面且不平行直线，则$l\bot\Gamma$ 证明：这个证明就和立体几何里的线面垂直类似了．设这三条直线的方向向量分别为$\vec{a},\vec{b},\vec{c}$，由于它们既不共面又不平行，那么$\Gamma$中的任意一条直线的方向向量$\vec{m}$都可以写成

且$\vec{l}\cdot\vec{a}=\vec{l}\cdot\vec{b}=\vec{l}\cdot\vec{c}=0$，所以有

因此$l\bot\Gamma$，证毕．

• 定理3-面胞平行判定（1）：如果平面$\alpha$中的两条相交直线平行于胞$\Gamma$，则$\alpha\parallel\Gamma$． 证明：设这两条直线为$l_{1}$和$l_{2}$．和立体几何类似，假设它们不平行，即存在直线$m$不平行于$\Gamma$，说明它与$\Gamma$有公共点，而面和胞相交一定交于一条直线，这时设$l=\Gamma\cap\alpha$，由于$l_{1}$和$l_{2}$相交，所以一定有一条直线与$l$相交，不妨设$A=l_{1}\cap l$，这说明$A=l_{1}\cap\Gamma$，与$l_{1}\parallel\Gamma$的条件相矛盾，因此假设错误．证毕．
• 定理4-面胞平行判定（2）：如果平面$\alpha$平行于胞$\Gamma$中的平面$\beta$，那么$\alpha\parallel\Gamma$． 证明：对于$\alpha$中的每条直线都平行于$\beta$，根据线胞平行判定，每条直线就都平行于$\Gamma$，于是$\alpha\parallel\Gamma$．证毕．
• 定理5-面胞垂直判定：如果平面$\alpha$过胞$\Gamma$的法线$l$，那么$\alpha\bot\Gamma$． 证明：

  

  设法线$l$的垂足为A，B为$\alpha$与$\Gamma$的交线上的动点，C在法线上，那么AB就是$\alpha$中的直线BC在$\Gamma$中的射影，$\angle ABC$就是直线$BC$与胞$\Gamma$的夹角，当B与A重合时这个夹角取最大值，为90度，这个最大值按照定义，就是面$\alpha$与$\Gamma$的面胞角大小．由于这个面胞角为90度，所以$\alpha\bot\Gamma$，证毕．
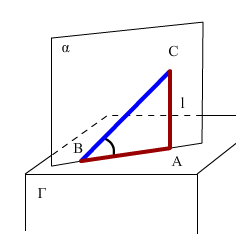
• 定理6-二胞平行判定（1）：如果胞$\Gamma$中的两个不平行的平面都平行于胞$\Delta$，那么$\Gamma\parallel\Delta$． 证明：略，类比定理3的证明．
• 定理7-二胞平行判定（2）：如果胞$\Gamma$中的三条不平形且不共面的直线都平行于胞$\Delta$，那么$\Delta\parallel\Gamma$． 证明：这三条直线可以确定两个不相互平行且都平行于$\Delta$的平面，由定理6就可以得出$\Delta\parallel\Gamma$．也可以类比定理3的证明．
• 定理8-二胞垂直判定：如果胞$\Gamma$过垂直于胞$\Delta$直线，那么$\Gamma\parallel\Delta$． 证明：略，类比定理5的证明．
• 定理9-半垂直的判定：同立体几何面面垂直的判定．
• 定理10-绝对垂直的判定：如果面$\alpha$中的两条相交直线都垂直于面$\beta$，那么$\alpha\top\beta$． 证明：我们同样使用向量法．设这两条相交直线的方向向量为$\vec{a}$和$\vec{b}$，面$\beta$中任意两条不平行的直线为$\vec{c}$和$\vec{d}$，则$\alpha$中任意直线的方向向量$\vec{l}_{1}$可表示为：

设$\vec{l}_{2}$为面$\beta$中的任意一条直线，并且$\vec{l}_{2}\cdot\vec{a}=\vec{l}_{2}\cdot\vec{b}=0$，所以

这就证明了$\alpha$中的任意一条直线都垂直于$\beta$．

下面我们来看一下其他的一些四维空间中的定理。

• 定理11-射影体积定理：胞$\Gamma$中某个图形在另一个胞$\Delta$中的射影与原图形的体积比为二胞角的余弦值． 证明：这个证明和三维的射影面积定理类似，把那个图形细分成很多个正方体微元，投影后的图形微元会在某个方向上压缩，如果把这个微元平移到交面处就会发现压缩后正方体的微元的一条边变短了，压缩的系数就是二胞角的余弦值．
• 定理12-线胞最小角定理：设$l_{1}$是直线$l$在胞$\Gamma$中的射影，$l_{2}$是胞中的某条直线，那么有

证明：我们可以先平移这三个直线使它们共点，此时它们一定共胞，然后再用立体几何的证明方法证明（略）．

• 定理13-面胞射影面积定理：和三维的射影面积定理一样，只不过是在胞内的射影． 证明：略，类比定理12的证明．
• 定理14-二面射影面积定理：一个平面中的任意图形在另一个平面中的射影的面积与原面积的比值等于这两个面间的最大角与最小角的余弦值的积． 证明：这个的证明过程我们稍微用了一点四维解析几何．我们设有一个在$Oxy$平面上的两个重合的平面$\alpha$和$\beta$，我们先把$\beta$在面$Oxz$中旋转$\theta_{1}$大小，再在$Oyt$面中旋转$\theta_{2}$．下面我们先证明$\theta_{1}$和$\theta_{2}$就是面$\alpha$和$\beta$所夹二面角的最大角和最小角． 先在$\alpha$上画一个单位圆，方程为

我们想要求出它在经历两次变换后在$Oxy$上的投影方程．我们先写出两次旋转变换的变换公式：

和

依次代入圆方程，我们得到惊喜的结果：

与我们期望的一样，这是一个椭圆方程．不妨设$\theta_{1}\gt\theta_{2}$，于是长短轴分别是$\cos\theta_{2}$和$\cos\theta_{1}$．

设想有一条长度为1的线段在变换后的平面上，它的一端在原点另一端在刚才那个单位圆上移动，那么它的投影就是一条一端在原点另一端在椭圆上的线段，这时它与$\alpha$的夹角的余弦值就是这个投影的长度．很明显，当投影是短轴时取得最大角$\theta_{1}$，当它是长轴时取得最小角$\theta_{2}$，因此$(\theta_{1},\theta_{2})$就是$\langle\alpha,\beta\rangle$（还记得吗，二面角大小是一个二元组）．

然后我们再来证明面积的关系．假设在$\beta$变换前它里面有一个在$Oxy$中坐标为$(a,b)$的点，它与坐标轴围成的矩形的面积为ab，那么经历了旋转变换后它的投影为$(a\cos\theta_{1},b\cos\theta_{2})$，矩形的面积变为了$ab\cos\theta_{1}\cos\theta_{2}$，面积比为$\cos\theta_{1}\cos\theta_{2}$．对于任意图形我们可以把它细分成无数多个这样的小矩形，每个矩形及其射影都满足这个面积比，因此整个图形同样满足．

综上所述，我们就证明了这个定理．

• 定理15：设$(\theta_{1},\theta_{2})$是面$\alpha$与$\beta$的二面角大小，$\gamma$是$\beta$的法平面，那么$\alpha$与$\gamma$的二面角大小为$({\pi \over 2}-\theta_{2},{\pi \over 2}-\theta_{1})$． 证明：我只想出用解析法证明，不过应该可以用几何法的．我们沿用上一个定理证明中的$\alpha$和$\beta$，再加上一个在$Ozt$中的面$\gamma$，由于$\gamma\top\alpha$，所以我们需要求出那个单位圆在$Ozt$上的投影，从而算出$\gamma$与$\alpha$的二面角． 在将单位圆方程做变换后消去x和y，我们就得到它在$\gamma$上的投影方程：

于是，我们得到$\langle\gamma,\beta\rangle$的余弦值为$\cos\theta_{1}^\prime=\sin\theta_{2}$和$\cos\theta_{2}^\prime=\sin\theta_{1}$． 所以$(\theta_{1}^\prime,\theta_{2}^\prime)=({\pi \over 2}-\theta_{2},{\pi \over 2}-\theta_{1})$． 好了，证明完毕．

• 定理16-线胞角的计算方法：直线$l$与胞$\Gamma$的夹角大小等于$l$与$\Gamma$的法线的夹角的余角。 证明：这个证明很简单，只需以直线$l$、$l$的射影、$\Gamma$的法线为三边作一个三角形就可以看出来了。
• 定理17-线胞三垂线定理：如果胞$\Gamma$中的直线$m$垂直于胞外直线$l$在胞中的射影，则$m\bot l$ 证明：略，类比立体几何中的三垂线定理。

我就暂时先写这么多了，以后我还会补充的．如果大家发现了新的定理也可以在留言里面告诉我哦．

这次来一个计算题吧，请计算正16胞体相邻两个胞之间的二胞角。

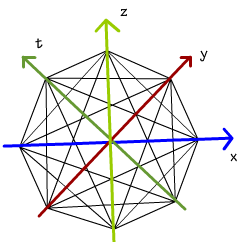
正16胞体是正八面体的类比，超立方体的对偶多胞体，即把超立方体每个胞的中心连起来就得到正十六胞体。

上次的答案：

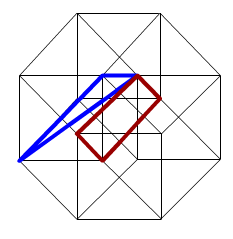
颜色与题中的面对应。 //蓝色那个找了好久。。。