丁仪摇摇头：“不可能的量子态只在无观察者的情况下呈现，观察者一出现它就塌缩为我们的经验现实，我们永远也不可能见到概率云。”

“装一台无人职守的摄象机不就行了吗？”中校说。

“摄象机也是观察者，同样会引起量子态的塌缩。这也是我让所有监视装置都关闭的原因。”

“可摄象机本身并没有意识啊。”林云说。

看看，是我唯心还是你唯心？观察者并不需要有意识。”丁仪对林云坏笑了一下。

这个精彩片段出自刘慈欣的小说《球状闪电》，它描述的就是量子力学中著名的哥本哈根诠释，即观察者的观察行为会影响量子的状态。

量子力学是我认为最神奇的学科了，它里面有很多违背常理的规律和结论，上面大刘说的就是使我困惑了很久的东西。量子真的是睁着眼睛就是粒子的，闭着眼睛就是概率云吗？怎么想都有种唯心的感觉。然而科学不是唯心的，任何东西的存在都有它存在的原因，波函数也是。终于，随着学习的深入，我逐渐明白了这背后的基本原理。下面我来给大家科普一下吧。

注：可能我的理解还存在一些问题，如果有异议欢迎在留言中和我探讨。

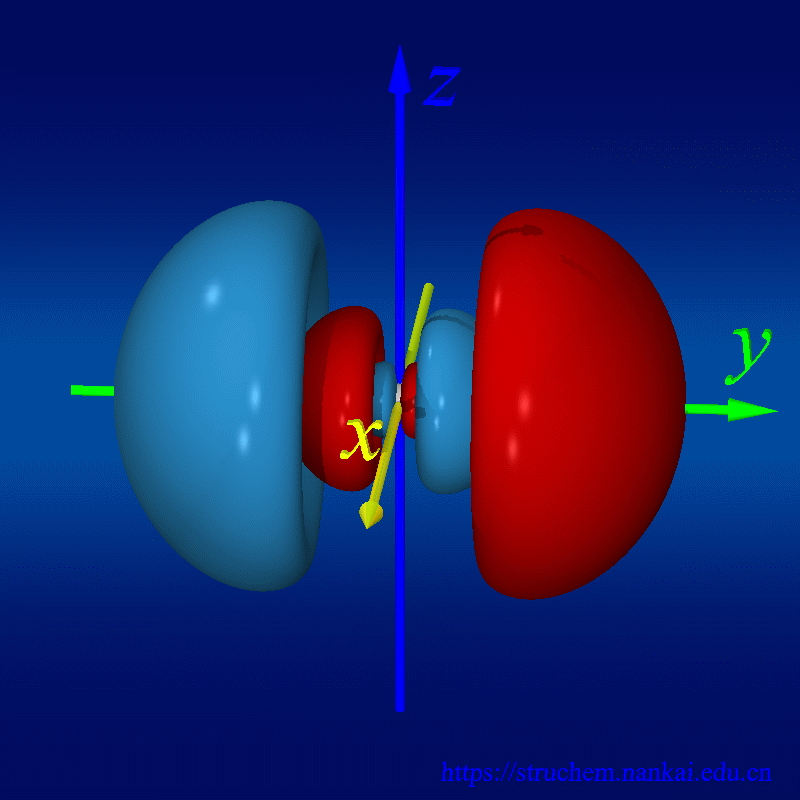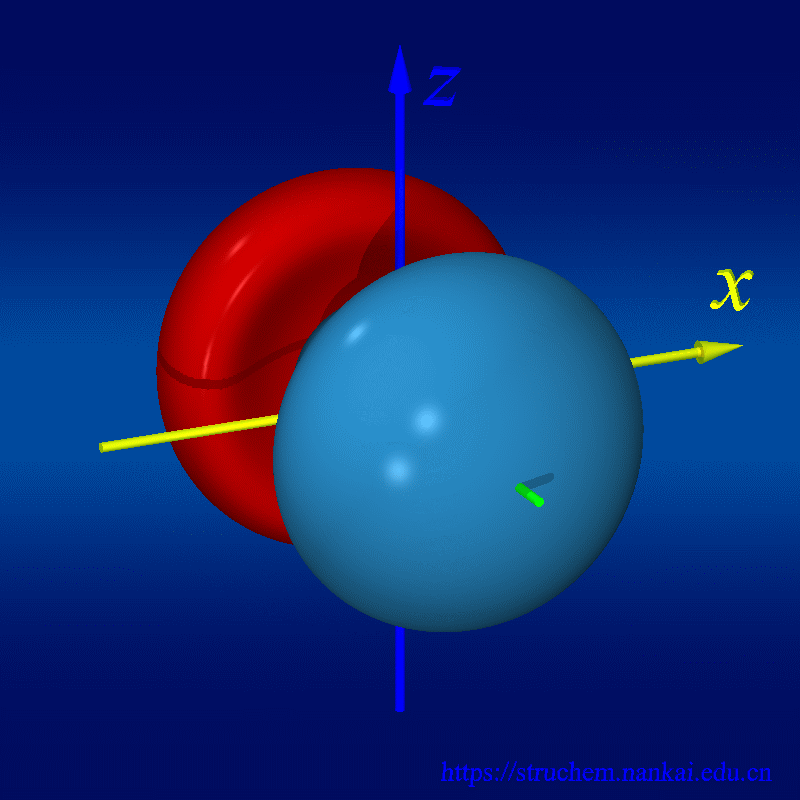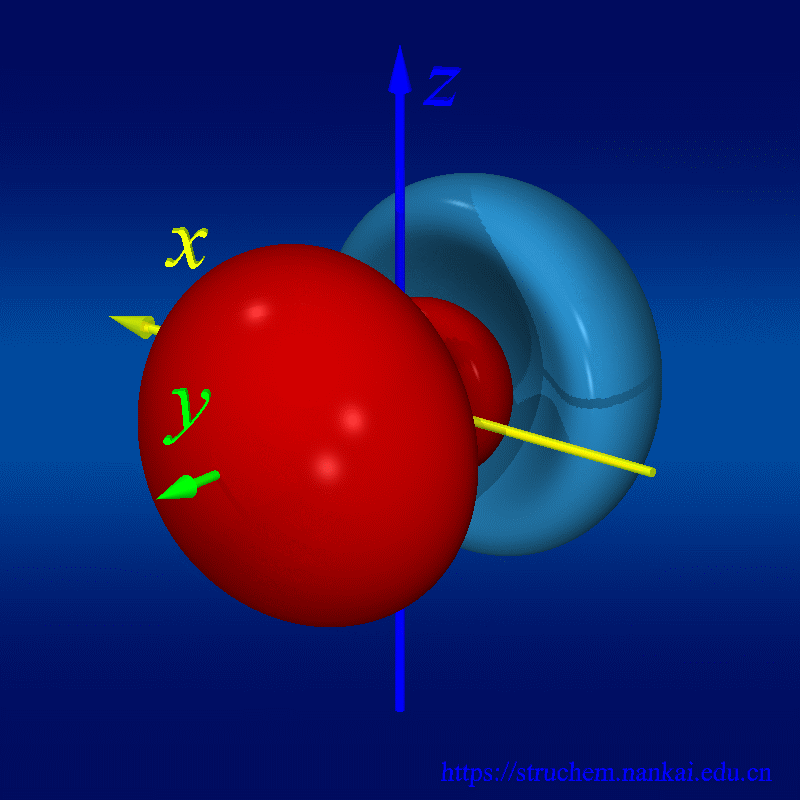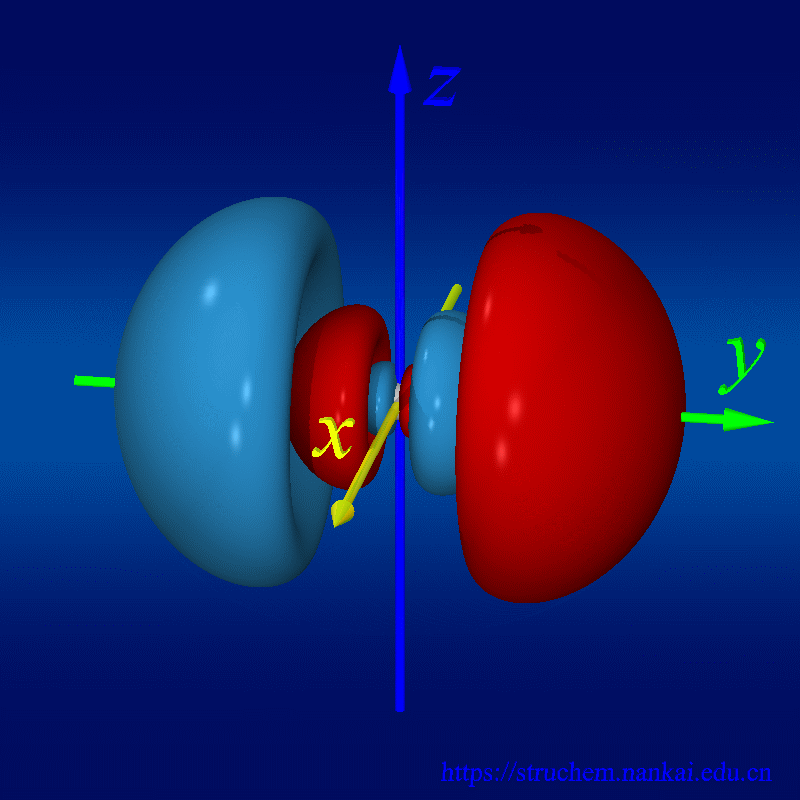
波函数是量子力学中最核心的东西之一。我们知道，量子具有不确定性原理，即你不能同时精确地确定一个粒子的位置和动量，而只能确定它们取一些值的概率，于是波函数也就诞生了。在量子力学中，一个波函数是一个自变量为坐标的函数，它模的平方就代表粒子处在不同坐标的概率密度。就像在牛顿力学里面我们可以通过求解根据牛顿第二定律列出的动力学方程来得出物体的运动方程一样，量子力学里面我们同个求解薛定谔方程来得到波函数，这时我们就确定了这个粒子在量子力学意义下的运动状态。我们高中化学里面讲的电子云就是一种波函数。波函数的自变量还不仅限于坐标，它还可以是其他变量，如自旋方向，偏振方向等。

好了，现在轮到哥本哈根诠释了。它是说测量的动作影响了系统，使得原本某物理量存在多种可能的量子态缩减成了这个物理量只存在一种可能的态（翻译的维基百科）。但是，该怎么理解这句话呢？真的如小说片段中描述的，你看宏电子实际就是观测它的位置，于是它的位置就变得确定，即一个实实在在的宏电子呈现在你面前，而不是它的波函数，它的路径也变得确定吗？

其实，我们的困惑点在于眼睛、照相机等看似并没有对宏电子造成影响，只是观测而已，怎么就导致它坍缩了呢？要回答这个问题，我们必须先搞清楚什么是观测，以及它造成的影响是什么。

我们在宏观世界里面看到一个物体，实际上是眼睛接收到了物体反射过来的光。也就是说，我们在用眼睛观察某个物体时，实际情况是这样的：光子与物体发生相互作用而被反射回来，此时物体由于相互作用已经不在原来的状态上了，它的状态信息已经转移到了光子上，之后光子再被我们的眼睛接收到，产生视觉。在我们的宏观世界中物体受光子的影响微乎其微，以至于可以忽略，而微观世界则不同了，光子将明显地改变被测物体的状态，新的状态就是物体的位置确定的态。当然，完全确定的状态其实是一种理想情况，实际到达的状态只可能是“不纯”的确定态，即谱线有一定的宽度。

关键是，所有的观测都将不可避免地影响到粒子的状态，一个粒子在经历一次观测后状态都将被改变，它到达的目标状态是由观测方式决定的，如我观测粒子的位置它就会到达位置为确定值的状态上，观测自旋方向就会使其到达自旋态确定的状态上。我们把这种粒子在经历观测后量子态发生改变的现象称为波函数坍缩，那个目标状态叫做本征态。而这个规律就导致了一个非常有实际价值的原理－－量子不可克隆原理，曾有人根据这个原理提出过可以完全消灭伪钞的量子钞票，这个想法给现代的量子信息学奠定了基础。假如我有一份机密信息想传递给A，我就把我的信息以量子态的形式保存在一些粒子中，然后传递给A，如果信息被人窃听了，那就会造成波函数坍缩，于是我们就有办法发现他。然而具体的做法比较复杂。

那么，观察者又是什么呢？其实例子挺多的，我们人本身就是一种复杂的观察者，其他的物体，如照相机、传感器、粒子探测器等都是观测者。实际上人这个观测者是很复杂的，人体内的每个原子和分子都是量子化的，而我们看到的东西却是经典的，这中间就涉及到量子与经典的过渡，所以我们暂时不讨论它，而来讨论一个相对简单而且大家应该都熟悉的观测者模型——单光子检偏实验，用到的材料是偏振片。

我们把一个偏振片放在一个胶片的前面，然后让它们两个的连线正对一个线偏振光源。这时我们知道，胶片的感光量会随偏振片的偏振取向和光源所发出的光的偏振取向的夹角变化而变化，当这两个方向平行时感光量最强，垂直时胶片不感光，任意夹角的情形可以通过马吕斯定律计算光强。这是经典情形。

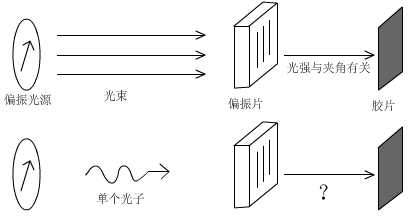
现在我们把那个光源改成单光子光源，即每次只发出一个光子，情形会有什么不同呢？我们知道光子的偏振可以沿两个相互垂直的方向分解，而任意的偏振态可以看成这两种的叠加态。此时这个设备就成了光子偏振态的观测者，当一个叠加态的光子通过这个设备时，只有两种可能：要么光子通过偏振片，使胶片感光，观测结果就是偏振态与偏振片平行；要么通不过，观测结果就是偏振与偏振片垂直。当光子通过偏振片后光子就会由于和偏振片中原子的相互作用而发生坍缩，由偏振既可能为与偏振片平行的又可能垂直的坍缩为这两种可能中的一种，从而要么使胶片感光，要么不感光。这就是最简单的波函数坍缩的例子。

好了，这下大家应该对波函数的坍缩有一种清晰的认识了吧。关于大刘的小说我就不多说了，因为宏电子的存在本身就属于纯科幻的，在根据目前的理论有很多说不通的地方，比如既然它的质量那么小，它对光子肯定很敏感，根本就不能反射回来一大堆光子使你的眼睛接收到，如果真的存在宏电子，那么在阳光下肯定被光子打得四处乱飞。当然，虽然大刘的小说存在一些漏洞，他依然是我最崇敬的科幻作家。

小说中丁仪还说，“我们永远也不可能见到概率云”，这是真的吗？答案是否定的！我们可以观测概率云，而且已经实现了，著名的量子围栏就是一个例子：

照片是扫描隧道显微镜下的48个Fe原子在Cu的表面排列成直径为14.3nm的圆圈构成一个“量子围栏”，照片中反映的是电子密度的高低，围栏内是电子密度波的驻波。

这是怎么做到的？为什么波函数没有坍缩？注意，当我观测相应的物理量时才会导致相应的波函数的坍缩，比如如果我观测的是位置，那么它的位置波函数就会坍缩。而如果我观测的东西就是粒子的概率密度呢？显然，我们就间接地观测到了概率云。由于量子围栏实验里面用的是扫描隧道显微镜（stm），它的原理是测定隧道电流的大小来计算出样品某处的高度，从而建立样品表面的三维模型，不过，根据量子力学我们可以知道这个电流的大小还会随电子的概率密度变化，这样就会使计算出来的高度随电子概率密度变化而变化，这样，我们就间接地“看”到了概率云了。