四维空间是我觉得最考想象力而又最有意思的东西了，它看不见摸不着，多出的一个维度却使它如此的令人着迷，科幻小说中也总少不了他的身影．那么研究它的几何肯定非常有意思，下面就让我们离开我们熟悉的三维空间，走进这个全新的空间吧．

这里先澄清一个常见的误区，就是很多人认为四维空间是三维空间加上时间维．这样的空间其实叫做四维时空，是为了研究相对论而提出的一种物理模型，它的性质在我以后的文章里面也会涉及到．而我们现在所说的四维是指纯几何的四维，即四个维度都是空间，所以和相对论没有联系．对于四维空间，我推荐一个数学科普视频《维度数学漫步》，其中的两集详细地讲了四维空间中的多面体．

在开始的这几篇文章中我主要是给出四维空间的一些直观的例子，让大家对四维空间有一个直观感受，之后再开始探讨四维欧氏几何，即线面关系、二面关系等．

四维空间其实没有想象中的那么难，只要有正确的研究方法．我们知道三维空间中再复杂的物体都是由正方体，长方体，圆柱等基本几何体构成的，只要能研究清楚这些基本物体的几何就可以搞清楚三维空间的性质．四维空间也一样．因此，我们的第一步就是要找出四维空间的基本几何体．

不像三维空间那样我们可以在头脑中直接想象出一个物体的形状，四维空间中的物体是抽象的，我们很难像直接像想象三维物体那样想象四维的物体，只能过一些间接的方法．这些方法主要分为分析四维空间的方法和可视化四维空间的方法．我们先来看一些例子：

类比法

类比法可是说是贯穿了整个四维空间的讨论方法，对于一个四维物体我们可以类比它从二维空间到三维空间的变化来类推它从三维空间到四维空间的变化．虽然这不是一种严密的证明方法，但它对找四维空间的感觉是很有用的．下面我们从两个重要的例子来了解一下类比法：

胞的概念

我们知道一维空间中虽然有直线，但直线就是空间本身，所以在一维空间讨论直线没有价值，只有在二维及以上的空间讨论才有意义；同样平面之于二维空间也是如此，二面关系只能到空间中讨论；空间之于三维空间也是如此，也就是说，四维空间中我们就需要考虑内嵌的三维空间了．我们也可以这样想：二维空间包含点和直线，三维空间包含点、直线和平面；那么四维空间就包含点、直线、平面和“三维切片”，我们把这种三维空间中所没有的新成员称为胞，它是三维的．二维空间中有多边形，三维空间有多面体，四维空间相应地有多胞体．

构造超立方体

现在来看第二个例子，我们来构造一个四维物体．我们现在知道一个零维的点平移3个单位可以成为一维的线，它有两个顶点；线平移可以成为一个正方形，它有四个顶点；正方形平移即正方体，有八个顶点；那么，继续类比下去，正方体平移就会成一个四维几何体，而且有16个顶点．好了，我们现在构造出了第一个四维几何体，我们把它叫做超立方体，它将成为我下一篇文章的重点．下面的图展示了上面的这个类比推理的过程．

大家也许会问，上面图中的那个超立方体画出来不也是一个三维物体吗？怎么会是四维物体呢？哈，我正要回答这个问题，因为图中的超立方体就是用了下面要讲的可视化方法：

投影法

由于我们的空间是三维的，四维物体根本就“放”不进来，就像你不能把一个立方体完全塞到一个平面里一样．那么我们怎么观察这些四维物体呢？我们是生活在三维空间中的，而我们看到的图像是二维的，即三维物体在平面上的投影．既然三维物体在平面上的投影是二维的，那么四维物体在三维空间中的投影就应该是三维的（注意，这里又用到了类比法），所以我们也可以看它们在三维空间中的投影．投影也分很多种，比如大家在上面那张图上看到的超立方体就是它在三维空间中的正交投影，即平行光照射下四维物体的“阴影”．类似的方法还有透视投影，即点光源下的阴影，只不过很少用到．下面我们重点说一下球极投影．

球极投影

虽然球极投影也不能展示出四维物体的真面目，但它却可以很直观的展示出几何体上顶点、棱以及面等几何元素的相对关系，这对我们对它的研究是很又帮助的．我们先来介绍一下三维空间中的球极投影吧

球极投影是一种把球面上的物体投影到平面上的方法．具体的做法是：将投影的目标平面与球体的南极相切，然后对于球面上的每一点，它的像点就是过它本事以及球面北极点的直线与平面的交点．说起来是有点绕，看一下上面那张图要好得多，把平面图想成三维的就可以了．这样，如果我们要给生活在二维空间中的生物展示三维几何体，我们只需将使几何体的所有顶点都放在球面上，然后将棱“膨胀”到球面上，然后再球极投影．我们发现球极投影的一个局限性：它要求物体的所有顶点都共球！即使这样，它仍然是一种很有用的方法，因为我们研究的都是正多胞体等顶点共球的物体．

四维球极投影就是以上方法在四维空间中的类比（看，又是类比法），把球面换成超球面，即球面的四维类比，平面换成我们所在的三维空间，然后被投影的三维物体换成四维物体，我们就可以看到它的球极投影了．下面，让我们来看一下一些四维正多胞体的球极投影：

这是四维单形，正四面体的类比。我们可以清楚的看到它有5个顶点，10条棱，9个面，然后这些面将空间划分成了5个区域，因此它有5个胞．注意这些本来是正多面体的胞在球极投影后变了形，但它依然是正多面体．

这是我们在上面看到的超立方体的球极投影．和我们类比出来的结果一样，它有16个顶点，32条棱，由内外大小两个正方体嵌套而成．

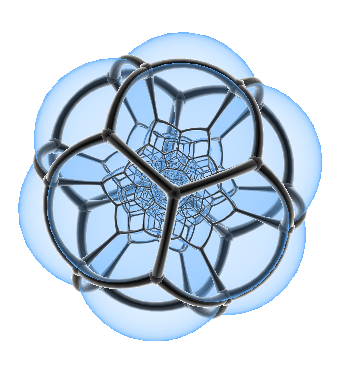
这是120号，正120胞体，正十二面体的类比．它一共有120个胞，因此得名．我们可以看到它内部有很复杂的结构，在接下来的文章中我们会深入讨论它的内部结构．

这是四维空间中最复杂的正多面体，600号．它是正二十面体的类比，一共有600个正四面体胞，与120号是对偶多胞体．它的结构是如此的复杂，以至于都有些看不清．

最后，来看看24号．这是一个很神奇的多胞体，因为它的三维类比菱形十二面体并不是正多面体，而它自己居然是！我们可以看到它的每个胞都是正八面体，在最中间有一个球形结构，仔细看它实际上是由四个圆框出来的一个截半立方体结构,它里面又套了一个小八面体．

截面法

截面法我们用到的相对比较少，这里还是简单介绍下．我们知道，在向二维生物们展示三维物体的时候，我们还可以采取一种更加直接的方式：将物体慢慢穿过二维平面，让生物们观察三维物体的截面．同样，对于四维物体我们也可以将它穿过我们的空间然后观察它们的截面动画，此时的截面就应该是三维的了．然而这是很困难的一件事，因为就算是给你看一个三维物体的截面动画你也很难想象出它的模样，更何况是四维物体．虽然这种方法对研究的帮助不大，但对于找感觉还是有点用处的．比如，按照类比法，一个四维单形正着穿过三维空间的动画就是一个很小的正四面体慢慢长大，然后突然消失．你能想出超立方体的截面动画吗？

左面是一个24号穿过三维空间时的截面动画。

好了，现在你的思维已经具备进入四维空间的条件了，下一篇系列文章中我们将从超立方体入手，着重探讨四维空间基本元素的相对位置关系，准备好了吗？